30 Is What Percent Of 50
News Co
Apr 05, 2025 · 5 min read
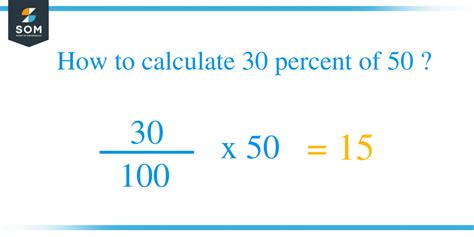
Table of Contents
30 is What Percent of 50? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to more complex financial analyses and scientific studies. Understanding how to solve percentage problems is crucial for making informed decisions and navigating numerical data effectively. This comprehensive guide will delve into the question, "30 is what percent of 50?", providing a detailed step-by-step solution, exploring different calculation methods, and offering practical examples to solidify your understanding.
Understanding Percentages
Before diving into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred" or "out of a hundred". For instance, 50% means 50 out of 100, which can be represented as the fraction 50/100 or the decimal 0.50.
Calculating "30 is What Percent of 50?"
There are several approaches to solving this percentage problem. Let's explore the most common methods:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 30
- Whole: 50
Substituting these values into the formula, we get:
(30 / 50) * 100% = 60%
Therefore, 30 is 60% of 50.
Method 2: Setting up a Proportion
Another effective way to solve this problem involves setting up a proportion:
30/50 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
30 * 100 = 50 * x
3000 = 50x
x = 3000 / 50
x = 60
Therefore, x = 60%, confirming that 30 is 60% of 50.
Method 3: Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100%.
First, express the relationship as a fraction: 30/50
Next, simplify the fraction: 30/50 simplifies to 3/5
Then, convert the fraction to a decimal: 3 divided by 5 equals 0.6
Finally, multiply the decimal by 100% to express it as a percentage: 0.6 * 100% = 60%
Again, this confirms that 30 is 60% of 50.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just an academic exercise; it's a vital skill with practical applications across numerous fields:
Finance and Budgeting:
- Calculating discounts: Imagine a store offering a 20% discount on a $50 item. Using percentage calculations, you can quickly determine the discount amount ($10) and the final price ($40).
- Understanding interest rates: Percentage calculations are fundamental to comprehending interest rates on loans, mortgages, savings accounts, and investments. Knowing how to calculate interest helps you make informed financial decisions.
- Analyzing financial statements: Percentage changes in revenue, expenses, and profits are crucial for assessing business performance and making strategic plans.
Everyday Shopping:
- Comparing prices: Percentages help you compare prices and identify the best deals. For example, determining which product offers a better value based on unit price or comparing discounts expressed as percentages.
- Calculating sales tax: Understanding how sales tax is calculated as a percentage of the purchase price is essential for budgeting and accurately determining the total cost of goods.
- Tip calculation: Calculating a tip as a percentage of the bill is a common application of percentage calculations in daily life.
Science and Research:
- Analyzing data: Scientists and researchers use percentages to analyze data sets, present findings, and express the relative frequency of events or characteristics within a population.
- Expressing experimental results: Percentage changes or differences in experimental results are essential for demonstrating the significance of findings.
- Statistical analysis: Percentages are crucial for understanding various statistical concepts such as proportions, probabilities, and confidence intervals.
Education and Academics:
- Calculating grades: Many grading systems use percentages to represent a student's performance on assignments and tests, culminating in a final percentage grade.
- Interpreting test scores: Percentage scores on standardized tests are widely used to compare student performance across different schools and populations.
- Expressing research results: Academic research often employs percentages to represent the results of surveys, experiments, and analyses.
Advanced Percentage Calculations
While the calculation "30 is what percent of 50?" demonstrates a basic percentage problem, understanding how to handle more complex scenarios is beneficial. Let's consider some extensions:
Finding the Whole when Given the Part and Percentage:
For example, if you know that 40% of a number is 20, how do you find the original number (the whole)? You can use the following formula:
Whole = (Part / Percentage) * 100
In this instance:
Whole = (20 / 40) * 100 = 50
Therefore, the original number is 50.
Finding the Part when Given the Whole and Percentage:
If you know that 75% of a number is 150, how do you find 75% of that number? Use this formula:
Part = (Percentage / 100) * Whole
In this instance:
Part = (75 / 100) * 150 = 112.5
Therefore, 75% of that number is 112.5
Percentage Increase or Decrease:
Calculating percentage increase or decrease is crucial for analyzing changes over time. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
A positive result indicates an increase, while a negative result indicates a decrease.
For example, if a value increases from 50 to 75, the percentage increase is:
Percentage Increase = [(75 - 50) / 50] * 100 = 50%
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The key to mastering any mathematical skill is consistent practice. Work through various problems to build your confidence and proficiency.
- Use Different Methods: Try solving problems using different methods (formula, proportion, decimal conversion) to understand the concepts from multiple perspectives.
- Check Your Answers: Always check your answers to ensure accuracy. You can do this by working backward or using a different calculation method.
- Visual Aids: Diagrams and charts can be helpful in visualizing percentage problems, particularly when dealing with complex scenarios.
- Online Resources: Numerous online resources, tutorials, and calculators are available to help you learn and practice percentage calculations.
Conclusion
The question "30 is what percent of 50?" provides a straightforward introduction to percentage calculations. However, this guide demonstrates that the application of percentage calculations extends far beyond simple arithmetic. By understanding the underlying principles and mastering various calculation methods, you equip yourself with a powerful tool for navigating the numerical world and making informed decisions in diverse contexts, from personal finance to scientific research. The ability to effortlessly calculate and interpret percentages is an invaluable asset in both personal and professional life. Remember to practice regularly and explore different approaches to solidify your understanding and confidence in handling percentage problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about 30 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.