33 And 1/3 As A Fraction
News Co
Mar 25, 2025 · 4 min read
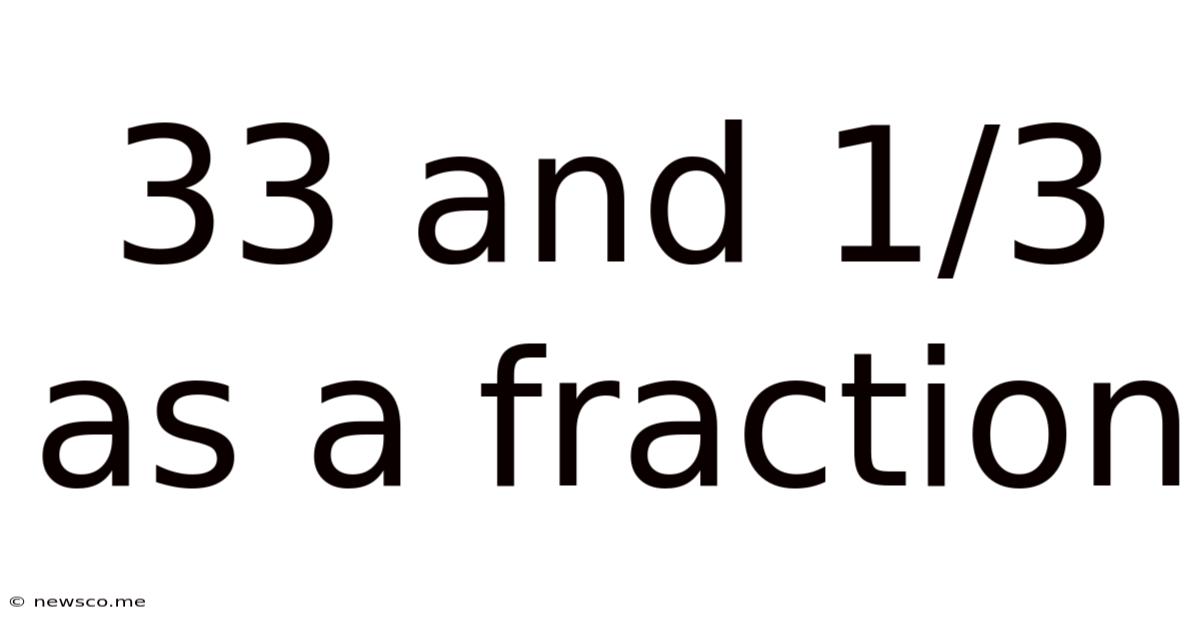
Table of Contents
33 and 1/3 as a Fraction: A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific concepts. This comprehensive guide delves into the representation and manipulation of mixed numbers, specifically focusing on converting the mixed number 33 and 1/3 into its fractional equivalent. We'll explore the underlying principles, provide step-by-step instructions, and offer practical examples to solidify your understanding.
Understanding Mixed Numbers and Improper Fractions
Before diving into the conversion process, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 33 and 1/3. An improper fraction, on the other hand, has a numerator (the top number) that is larger than or equal to its denominator (the bottom number). Converting a mixed number to a fraction involves transforming it into an improper fraction.
Why use improper fractions? Improper fractions are often preferred in mathematical operations, especially when multiplying or dividing fractions. They provide a more streamlined approach to calculations.
Converting 33 and 1/3 to an Improper Fraction: A Step-by-Step Guide
The conversion process involves two simple steps:
Step 1: Multiply the whole number by the denominator.
In our case, the whole number is 33, and the denominator of the fraction 1/3 is 3. Therefore, we multiply 33 by 3:
33 * 3 = 99
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 1. We add this to the result from Step 1 (99):
99 + 1 = 100
Step 3: Keep the denominator the same.
The denominator remains unchanged throughout the conversion process. Therefore, the denominator remains 3.
Final Result:
Combining the results from Steps 2 and 3, we obtain the improper fraction:
100/3
Therefore, 33 and 1/3 is equivalent to the improper fraction 100/3.
Practical Applications and Examples
Understanding the conversion of mixed numbers to improper fractions is essential in various mathematical contexts. Here are a few examples:
Example 1: Adding Mixed Numbers
Let's say you need to add 33 and 1/3 to 5 and 2/3. It's significantly easier to add these as improper fractions:
- 33 and 1/3 = 100/3
- 5 and 2/3 = 17/3
Adding the improper fractions:
100/3 + 17/3 = 117/3 = 39
Therefore, 33 and 1/3 + 5 and 2/3 = 39. This is far simpler than attempting to add them directly as mixed numbers.
Example 2: Multiplying Mixed Numbers
Multiplying mixed numbers is also much easier using improper fractions. Let's multiply 33 and 1/3 by 2:
- 33 and 1/3 = 100/3
Multiplying the improper fraction by 2:
(100/3) * 2 = 200/3 = 66 and 2/3
This calculation is far more straightforward than trying to multiply the mixed number directly.
Example 3: Dividing Mixed Numbers
Division of mixed numbers similarly benefits from conversion to improper fractions. Let's divide 33 and 1/3 by 5:
- 33 and 1/3 = 100/3
Dividing the improper fraction by 5:
(100/3) / 5 = 100/15 = 20/3 = 6 and 2/3
Again, the improper fraction approach simplifies the calculation significantly.
Beyond the Basics: Simplifying Improper Fractions
While 100/3 is a perfectly valid improper fraction representing 33 and 1/3, it's sometimes beneficial to simplify fractions when possible. However, in this specific case, 100 and 3 share no common factors other than 1, meaning the fraction is already in its simplest form.
Simplifying fractions involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, if we had the fraction 12/18, the GCD is 6. Dividing both the numerator and the denominator by 6 gives us the simplified fraction 2/3.
The Importance of Understanding Fractions in Real-World Applications
The ability to manipulate fractions is crucial in numerous everyday scenarios:
- Cooking and Baking: Recipes often require fractional measurements of ingredients.
- Construction and Engineering: Precise measurements and calculations are fundamental to these fields.
- Finance and Accounting: Understanding percentages and proportions is vital for financial literacy.
- Science and Technology: Fractions are used extensively in scientific calculations and data analysis.
Conclusion: Mastering the Conversion of Mixed Numbers to Improper Fractions
Converting mixed numbers like 33 and 1/3 to their improper fraction equivalents (100/3) is a fundamental skill in mathematics. This process simplifies calculations, especially when adding, subtracting, multiplying, or dividing fractions. The steps are straightforward, and mastering them will enhance your mathematical abilities and proficiency in various real-world applications. Remember the key steps: multiply the whole number by the denominator, add the numerator, and retain the original denominator. Practice these steps regularly to solidify your understanding and improve your problem-solving skills. By understanding fractions thoroughly, you'll be better equipped to tackle more complex mathematical challenges and apply your knowledge effectively in various aspects of your life. This foundational understanding of fractions will serve as a solid base for more advanced mathematical concepts and problem-solving in the future. Continue to explore and practice these essential skills to strengthen your mathematical proficiency and confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about 33 And 1/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.