36 7 As A Mixed Number
News Co
Apr 27, 2025 · 5 min read
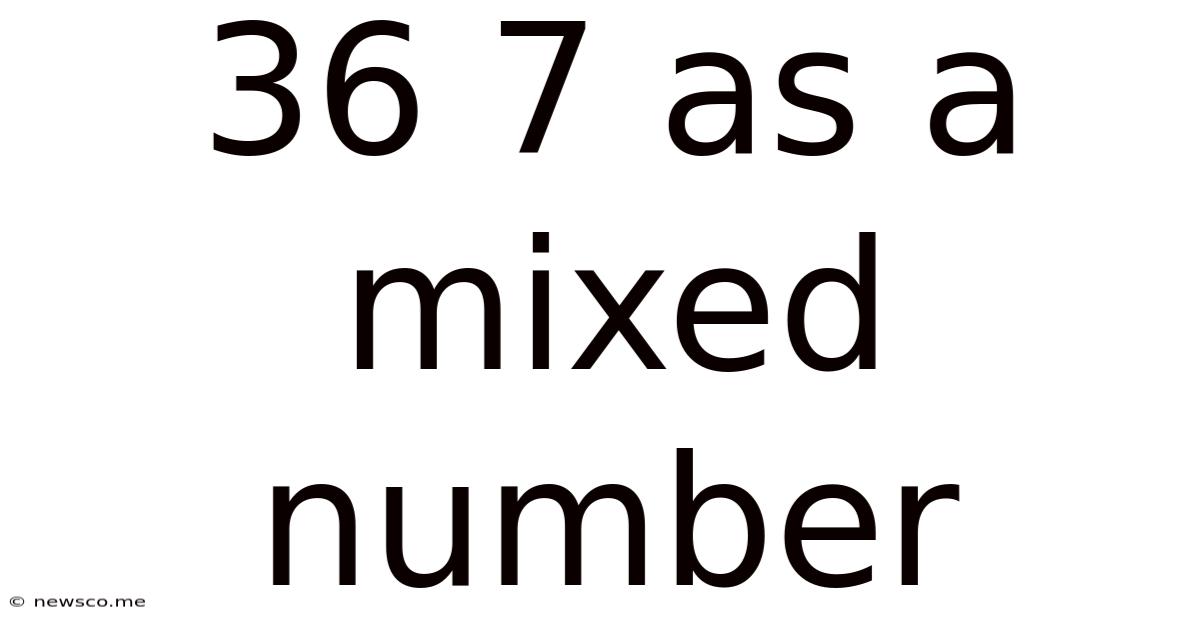
Table of Contents
36/7 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 36/7 into a mixed number, explaining the concept in detail and providing various examples to solidify your understanding. We'll also explore the broader context of fractions and mixed numbers, touching upon their applications in everyday life and more advanced mathematical concepts.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅔, and 5 ⅛ are all mixed numbers. They represent a quantity greater than one whole unit.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. The fraction 36/7 is an improper fraction because the numerator (36) is larger than the denominator (7). To convert an improper fraction to a mixed number, we need to determine how many times the denominator goes into the numerator and what the remainder is.
The Process: Step-by-Step
Let's convert 36/7 into a mixed number using a step-by-step approach:
-
Divide the numerator by the denominator: Divide 36 by 7. 36 ÷ 7 = 5 with a remainder of 1
-
The quotient becomes the whole number: The quotient (the result of the division) is 5. This becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the proper fraction: The remainder is 1. This becomes the numerator of the fraction part of our mixed number.
-
The denominator remains the same: The denominator of the fraction in the mixed number stays the same as the denominator of the original improper fraction, which is 7.
-
Combine the whole number and the fraction: Putting it all together, we get the mixed number 5 1/7.
Therefore, 36/7 = 5 1/7
Visualizing the Conversion
Imagine you have 36 cookies, and you want to divide them equally among 7 friends. You can give each friend 5 cookies (5 x 7 = 35 cookies). You'll have 1 cookie left over. This leftover cookie represents the remaining fraction, 1/7. So, you've given each friend 5 whole cookies and a 1/7 of a cookie. This visually represents the mixed number 5 1/7.
Converting Mixed Numbers back to Improper Fractions
It's crucial to understand the reverse process as well. To convert a mixed number back into an improper fraction, follow these steps:
-
Multiply the whole number by the denominator: In our example, 5 (whole number) x 7 (denominator) = 35
-
Add the numerator to the result: 35 + 1 (numerator) = 36
-
The result becomes the new numerator: 36 becomes the numerator of the improper fraction.
-
The denominator remains the same: The denominator remains 7.
Therefore, the improper fraction is 36/7. This confirms our conversion from improper fraction to mixed number and vice-versa.
Real-World Applications of Mixed Numbers
Mixed numbers are used extensively in various real-world situations:
-
Measurement: Measuring ingredients in a recipe (e.g., 2 ½ cups of flour) or calculating lengths and distances (e.g., 3 ¼ inches).
-
Time: Expressing durations (e.g., 1 ½ hours) or working with time zones.
-
Construction and Engineering: Precise measurements are crucial in these fields, often requiring the use of mixed numbers for accurate calculations.
-
Everyday life: Sharing items, calculating portions, and various other daily tasks may involve the use of mixed numbers.
Beyond the Basics: Working with Mixed Numbers
Once you understand the basics of converting between improper fractions and mixed numbers, you can move on to more complex operations:
-
Addition and Subtraction: Adding or subtracting mixed numbers requires converting them to improper fractions, performing the operation, and then converting the result back to a mixed number if necessary.
-
Multiplication and Division: Similar to addition and subtraction, it's often easier to convert mixed numbers to improper fractions before performing multiplication or division.
-
Comparing Mixed Numbers: To compare mixed numbers, you can compare the whole number parts first, and if they are equal, then compare the fractional parts.
-
Simplifying Mixed Numbers: Always simplify the fractional part of the mixed number to its lowest terms. For example, 5 2/4 should be simplified to 5 ½.
Advanced Concepts and Applications
Understanding improper fractions and mixed numbers forms the foundation for more advanced mathematical concepts:
-
Algebra: Solving equations involving fractions and mixed numbers.
-
Calculus: Working with derivatives and integrals that involve fractional expressions.
-
Geometry: Calculating areas, volumes, and other geometric properties often involves fractions and mixed numbers.
Practicing Your Skills
The best way to master converting improper fractions to mixed numbers is through consistent practice. Try converting several improper fractions to mixed numbers, and then convert those mixed numbers back to improper fractions. This will reinforce your understanding and build your confidence. You can find numerous online resources and workbooks with practice problems to further enhance your skills.
Conclusion
Converting the improper fraction 36/7 to the mixed number 5 1/7 is a straightforward process that relies on understanding the relationship between whole numbers and fractions. Mastering this conversion is vital for success in various mathematical contexts and real-world applications. By understanding the underlying principles and practicing regularly, you can confidently navigate the world of fractions and mixed numbers. Remember to always simplify your answers to their lowest terms for the most accurate and efficient results. This comprehensive guide provides a solid foundation for further exploration and mastery of this essential mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about 36 7 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.