36x 8y2 When X 3 And Y 6
News Co
Mar 24, 2025 · 5 min read
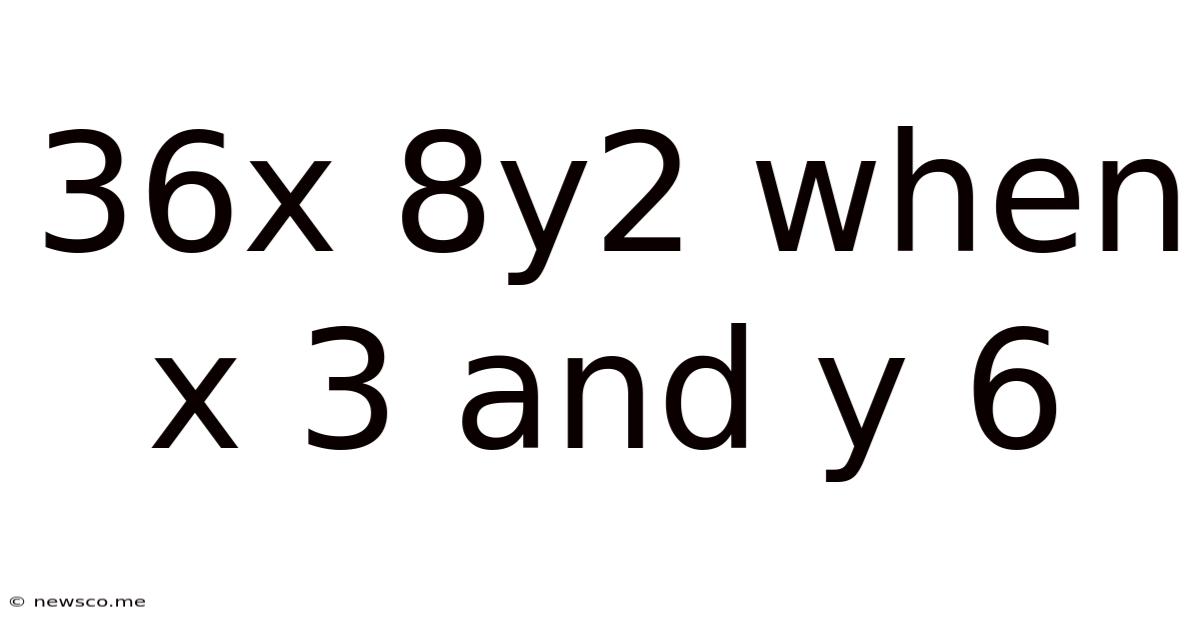
Table of Contents
Decoding 36x + 8y² When x = 3 and y = 6: A Comprehensive Guide
This article delves deep into the mathematical expression 36x + 8y², providing a step-by-step solution when x = 3 and y = 6. We'll not only calculate the final answer but also explore the underlying principles of algebraic substitution and order of operations (PEMDAS/BODMAS). Furthermore, we’ll examine how this simple equation can be applied in various real-world scenarios and expand on related mathematical concepts.
Understanding the Expression: 36x + 8y²
The expression 36x + 8y² is an algebraic expression containing two variables, x and y. The expression involves two basic operations:
- Multiplication: 36 is multiplied by x, and 8 is multiplied by y².
- Addition: The results of the multiplications are added together.
The term y² signifies 'y squared', meaning y multiplied by itself (y * y). This is an example of exponentiation, another fundamental arithmetic operation.
Substituting the Values: x = 3 and y = 6
The problem states that x = 3 and y = 6. This means we need to substitute these values into the expression. Substitution is a crucial technique in algebra, allowing us to evaluate expressions and solve equations.
Replacing x with 3 and y with 6 in the expression 36x + 8y², we get:
36(3) + 8(6)²
Applying the Order of Operations (PEMDAS/BODMAS)
To correctly evaluate the expression, we must follow the order of operations. This is commonly remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same order.
In our expression, 36(3) + 8(6)², the order of operations dictates that we tackle the operations in this sequence:
-
Exponents: First, we calculate 6². 6² = 6 * 6 = 36.
Our expression now becomes: 36(3) + 8(36)
-
Multiplication: Next, we perform the multiplications:
- 36(3) = 108
- 8(36) = 288
The expression simplifies to: 108 + 288
-
Addition: Finally, we add the two results together:
108 + 288 = 396
Therefore, the value of the expression 36x + 8y² when x = 3 and y = 6 is 396.
Expanding on Related Concepts
This seemingly simple problem allows us to explore several crucial mathematical concepts:
1. Variables and Constants: In the expression 36x + 8y², x and y are variables, representing unknown quantities. The numbers 36 and 8 are constants, their values remain fixed.
2. Algebraic Expressions and Equations: 36x + 8y² is an algebraic expression, a combination of variables, constants, and mathematical operations. If we set this expression equal to a value (e.g., 36x + 8y² = 396), it becomes an algebraic equation.
3. Linear and Non-linear Expressions: This expression is a non-linear expression due to the presence of the squared term (y²). Linear expressions only have variables raised to the power of 1 (e.g., 36x + 8y). The presence of the squared term introduces curvature when graphed.
4. Functions: We can consider this expression as a function of two variables, f(x, y) = 36x + 8y². This means the output (the value of the expression) depends on the input values of x and y. We evaluated the function at the point (3, 6).
5. Polynomials: The expression is a polynomial. Specifically, it's a polynomial in two variables. Polynomials are algebraic expressions involving only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables.
Real-World Applications
While seemingly abstract, this type of algebraic manipulation appears frequently in real-world applications:
-
Geometry and Area Calculations: The expression could represent the area of a combined shape. Imagine a rectangle with sides 36x and y, and a square with side length y. The total area would be 36xy + y². If x=3 and y=6, the area is calculated similarly.
-
Physics and Engineering: Many physics formulas involve similar expressions to model relationships between variables such as velocity, acceleration, and time.
-
Finance and Economics: Calculations involving compound interest or financial models frequently use algebraic expressions to relate different financial variables.
-
Computer Programming: Programmers use algebraic expressions extensively to create algorithms and perform calculations. The process of substitution is fundamental in programming loops and conditional statements.
Expanding the Problem: Exploring Different Values of x and y
Let's examine the impact of changing the values of x and y:
-
If x = 6 and y = 3: 36(6) + 8(3)² = 216 + 72 = 288. This demonstrates that changing the input values significantly alters the output.
-
If x = 0 and y = 0: 36(0) + 8(0)² = 0. This highlights the concept of the expression having a zero value under certain input conditions.
-
If x = -3 and y = 6: 36(-3) + 8(6)² = -108 + 288 = 180. This shows that negative values for x can affect the output.
-
If x = 3 and y = -6: 36(3) + 8(-6)² = 108 + 288 = 396. Note that squaring a negative number results in a positive number, thus not altering the final outcome.
Further Exploration: Graphing the Expression
For a more visual understanding, we can consider graphing the expression. Since it involves two variables, this would require a three-dimensional graph. The graph would show how the value of the expression changes as x and y vary. This visualization would help demonstrate the non-linear relationship between the variables. Plotting several points with different x and y values would further illuminate this relationship.
Conclusion
The seemingly simple algebraic expression 36x + 8y² offers a gateway into several crucial mathematical concepts. By substituting specific values for x and y, applying the order of operations correctly, and understanding the underlying principles, we can evaluate the expression accurately. Furthermore, by exploring variations in the input values and considering real-world applications, we deepen our understanding of the power and versatility of algebraic manipulation. This foundation is crucial for tackling more complex mathematical problems and applications in diverse fields. The solution, 396, is only one piece of a much larger mathematical puzzle, which reveals itself through deeper exploration and analysis.
Latest Posts
Related Post
Thank you for visiting our website which covers about 36x 8y2 When X 3 And Y 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.