37/6 Reduced To A Mixed Number
News Co
May 08, 2025 · 5 min read
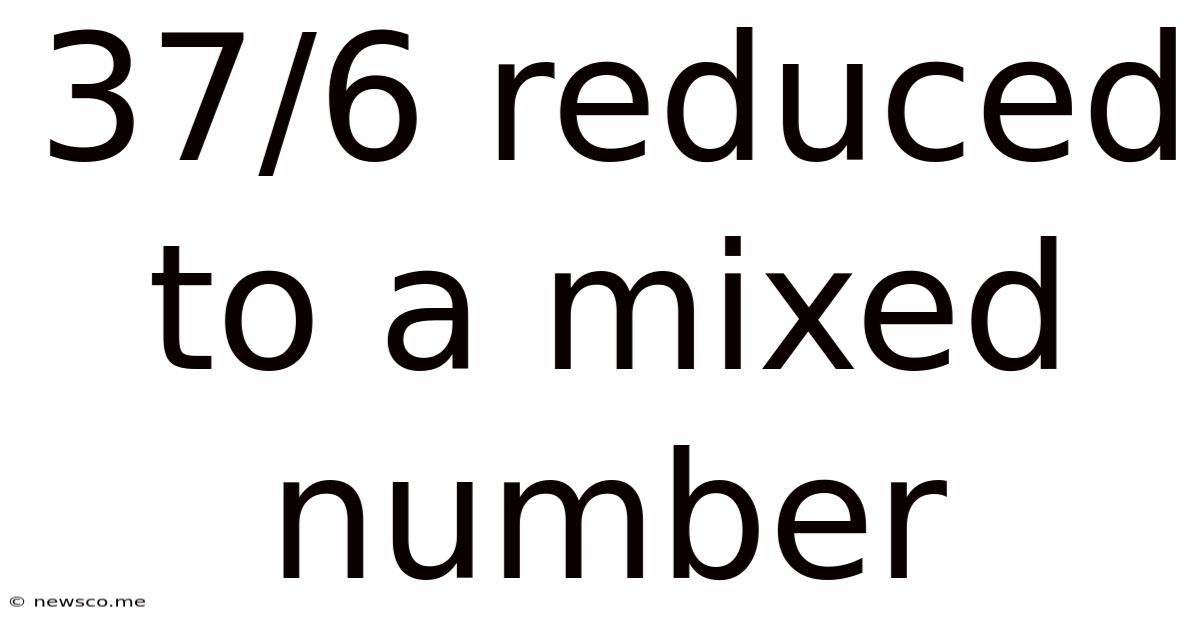
Table of Contents
37/6 Reduced to a Mixed Number: A Comprehensive Guide
Understanding how to convert an improper fraction, like 37/6, into a mixed number is a fundamental skill in mathematics. This process is crucial for various applications, from basic arithmetic to more advanced mathematical concepts. This comprehensive guide will walk you through the steps involved in reducing 37/6 to a mixed number, explaining the underlying principles and providing practical examples to solidify your understanding. We'll also explore the broader context of fractions and mixed numbers, demonstrating their importance in everyday life and various fields.
Understanding Fractions and Mixed Numbers
Before diving into the conversion process, let's establish a clear understanding of fractions and mixed numbers.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator shows how many of those parts are being considered. For instance, in the fraction 3/4, the whole is divided into four equal parts, and we're considering three of them.
Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 37/6 is an example of an improper fraction because 37 (numerator) is larger than 6 (denominator). Improper fractions represent a value greater than or equal to one.
Mixed Numbers: A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator. Mixed numbers provide a more intuitive way to represent values greater than one. For example, 6 1/2 is a mixed number representing six whole units and one-half of another unit.
Converting 37/6 to a Mixed Number: A Step-by-Step Guide
The conversion of 37/6 to a mixed number involves dividing the numerator (37) by the denominator (6). Here's how it's done:
Step 1: Perform the Division
Divide the numerator (37) by the denominator (6):
37 ÷ 6 = 6 with a remainder of 1
Step 2: Identify the Whole Number and Remainder
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 6. The remainder is the numerator of the fractional part of the mixed number. Here, the remainder is 1.
Step 3: Construct the Mixed Number
Combine the whole number and the remainder to form the mixed number. The remainder becomes the numerator, and the original denominator remains the same. Therefore, 37/6 as a mixed number is:
6 1/6
This means that 37/6 represents six whole units and one-sixth of another unit.
Practical Applications and Real-World Examples
The conversion of improper fractions to mixed numbers has numerous practical applications in various fields:
-
Baking and Cooking: Recipes often require fractional amounts of ingredients. Converting improper fractions to mixed numbers makes it easier to measure ingredients accurately. For instance, a recipe might call for 13/4 cups of flour, which is more easily understood and measured as 3 1/4 cups.
-
Construction and Engineering: Precision is crucial in construction and engineering. Converting fractions to mixed numbers helps ensure accurate measurements and calculations. For instance, calculating the length of a beam might involve converting an improper fraction representing inches into a mixed number for easier comprehension.
-
Time Management: Time is often expressed using fractions and mixed numbers. For example, 1 hour and 45 minutes can be expressed as 1 3/4 hours. Converting between these formats helps in efficient time management.
-
Data Analysis and Statistics: When dealing with data involving fractions, converting them to mixed numbers can improve readability and understanding. This is particularly useful when presenting data visually in charts and graphs.
-
Everyday Calculations: Many everyday situations involve calculations with fractions. For instance, sharing a pizza among friends, determining the amount of paint needed for a project, or calculating the cost of items on sale often requires converting between fractions and mixed numbers.
Expanding on Fraction Concepts: Equivalent Fractions and Simplification
While we've focused on converting 37/6 to a mixed number, it's beneficial to understand related concepts like equivalent fractions and simplification.
Equivalent Fractions: Equivalent fractions represent the same value but have different numerators and denominators. For example, 1/2, 2/4, and 3/6 are all equivalent fractions. They all represent one-half. Understanding equivalent fractions is crucial for comparing and manipulating fractions effectively.
Simplification (Reducing Fractions): Simplifying a fraction means reducing it to its lowest terms. This is done by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. For example, 6/12 can be simplified to 1/2 by dividing both the numerator and denominator by 6 (their GCD). Simplifying fractions makes them easier to understand and work with.
Beyond 37/6: Practicing Fraction Conversions
The process of converting improper fractions to mixed numbers applies to any improper fraction. Here are a few examples to practice:
-
22/5: Divide 22 by 5 (quotient = 4, remainder = 2). The mixed number is 4 2/5.
-
17/3: Divide 17 by 3 (quotient = 5, remainder = 2). The mixed number is 5 2/3.
-
41/8: Divide 41 by 8 (quotient = 5, remainder = 1). The mixed number is 5 1/8.
Regular practice is key to mastering this skill. You can create your own examples and practice converting various improper fractions to mixed numbers.
Conclusion: Mastering Fractions for Mathematical Proficiency
Converting improper fractions like 37/6 to mixed numbers is a fundamental skill in mathematics with broad applications in various aspects of life. By understanding the underlying principles and practicing regularly, you can confidently handle fraction conversions and apply them to solve real-world problems. Remember to break down the process into steps: division, identifying the whole number and remainder, and then constructing the mixed number. This comprehensive guide equipped you not just with the mechanics of the conversion but also with a deeper understanding of fractions and their significance. Continue practicing and exploring related concepts like equivalent fractions and simplification to strengthen your mathematical foundation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 37/6 Reduced To A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.