38 Is 95 Of What Number
News Co
Apr 27, 2025 · 5 min read
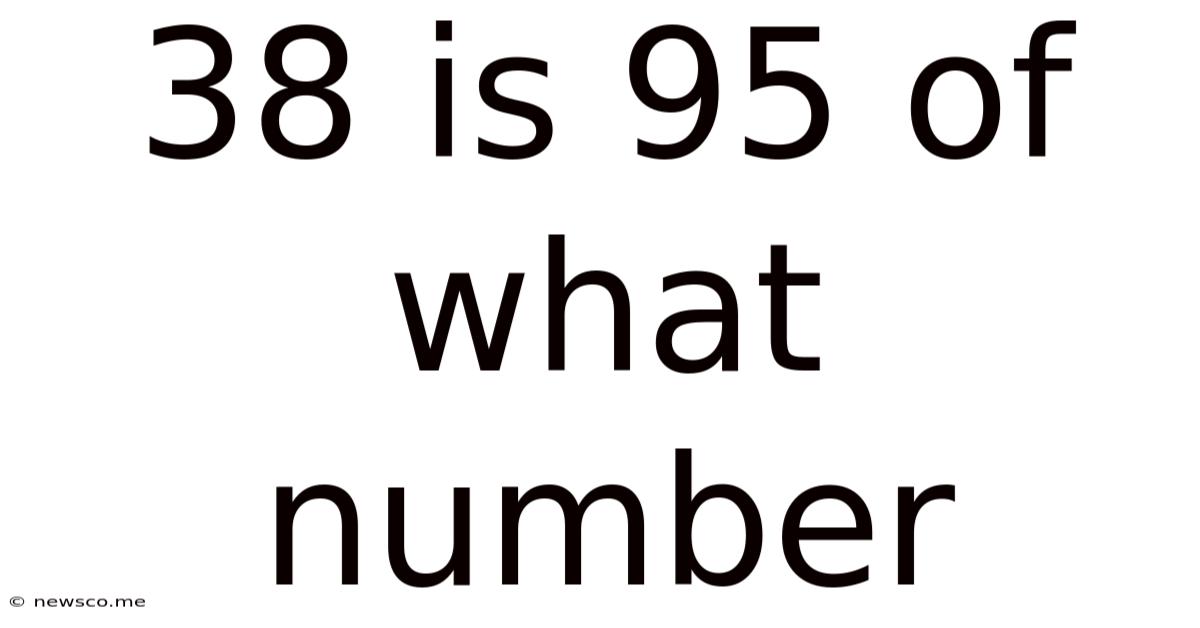
Table of Contents
38 is 95% of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific calculations. This article dives deep into how to solve the specific problem: "38 is 95% of what number?" We'll not only provide the solution but also equip you with the understanding and tools to tackle similar percentage problems with confidence. We'll explore various methods, emphasizing the underlying mathematical principles and providing practical applications.
Understanding the Fundamentals of Percentages
Before tackling the problem directly, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, which simplifies to ½ or 0.5.
Percentages are used extensively to represent proportions, changes, and rates. Understanding percentages allows you to:
- Compare quantities: Expressing values as percentages enables easy comparison, regardless of the original scale.
- Analyze data: Percentages help highlight trends and patterns within data sets.
- Make calculations: Percentage calculations are crucial in numerous financial, scientific, and everyday contexts.
Method 1: Using the Percentage Formula
The most straightforward method to solve "38 is 95% of what number?" involves using the fundamental percentage formula:
Part = Percentage × Whole
In our problem:
- Part: 38 (this is the given value)
- Percentage: 95% (or 0.95 as a decimal)
- Whole: This is the unknown value we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
38 = 0.95 × x
To solve for x, we need to isolate it:
x = 38 / 0.95
Calculating this gives us:
x = 40
Therefore, 38 is 95% of 40.
Method 2: Working with Fractions
Percentages can also be expressed as fractions. 95% can be written as 95/100, which simplifies to 19/20. We can then rewrite the problem as:
38 = (19/20) * x
To solve for x, multiply both sides by 20/19:
x = 38 * (20/19)
x = (38 * 20) / 19
x = 760 / 19
x = 40
Again, we find that x = 40. This method demonstrates the interchangeability between percentages and fractions in solving percentage problems.
Method 3: Using Proportions
Proportions provide another effective approach. We can set up a proportion based on the given information:
38/x = 95/100
This equation states that the ratio of 38 to the unknown number (x) is equal to the ratio of 95 to 100. To solve this proportion, we can cross-multiply:
38 * 100 = 95 * x
3800 = 95x
x = 3800 / 95
x = 40
Once more, we arrive at the solution x = 40. The proportion method is particularly useful for visualizing the relationship between the parts and the whole.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios. Here are some examples:
- Discounts and Sales: If a product is discounted by 20%, and the sale price is $60, you can use percentage calculations to find the original price.
- Tax Calculations: Determining the final price of an item after adding sales tax involves percentage calculations.
- Financial Investments: Calculating interest earned on savings accounts or investments relies on percentage calculations.
- Statistical Analysis: Percentages are frequently used to represent data in surveys, polls, and scientific research.
- Grade Calculations: Many educational systems use percentages to represent grades and academic performance.
- Business Metrics: Companies use percentages to track various key performance indicators (KPIs), such as conversion rates and profit margins.
- Scientific Measurements: Percentages are used in scientific experiments and data analysis to express the relative amounts of substances or changes in quantities.
Troubleshooting Common Mistakes
When working with percentages, several common mistakes can arise:
- Incorrect Decimal Conversion: Failing to correctly convert percentages to decimals (e.g., 95% to 0.95) is a frequent error. Remember to divide the percentage by 100 before using it in calculations.
- Mixing up Part and Whole: Ensure you correctly identify the 'part' and the 'whole' in the problem. The 'part' is the value that represents a portion of the 'whole'.
- Calculation Errors: Double-check your calculations to avoid simple arithmetic mistakes. Using a calculator can help improve accuracy.
- Incorrect Formula Application: Make sure you are using the correct percentage formula or method for the specific problem.
Expanding Your Percentage Skills
Mastering percentage calculations involves consistent practice and understanding the underlying principles. Here are some ways to improve your skills:
- Practice Regularly: Work through various percentage problems of different complexities.
- Use Multiple Methods: Try different methods (formula, fractions, proportions) to solve the same problem to reinforce your understanding.
- Solve Real-World Problems: Apply your knowledge to everyday situations, like calculating discounts or tips.
- Seek Help When Needed: Don't hesitate to ask for clarification or assistance if you encounter difficulties. Online resources, tutorials, and educational materials can be extremely helpful.
Conclusion
Solving "38 is 95% of what number?" demonstrates the application of fundamental percentage calculations. We explored three different methods—using the percentage formula, working with fractions, and employing proportions—to arrive at the solution of 40. This article not only provides the answer but also emphasizes the broader importance of understanding percentage calculations in various aspects of life. By mastering these skills and avoiding common mistakes, you can confidently tackle a wide range of percentage problems and apply your knowledge to real-world situations. Remember that consistent practice and a solid understanding of the underlying mathematical principles are key to success in this area.
Latest Posts
Related Post
Thank you for visiting our website which covers about 38 Is 95 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.