3x 2 X 4 X 2
News Co
Apr 23, 2025 · 5 min read
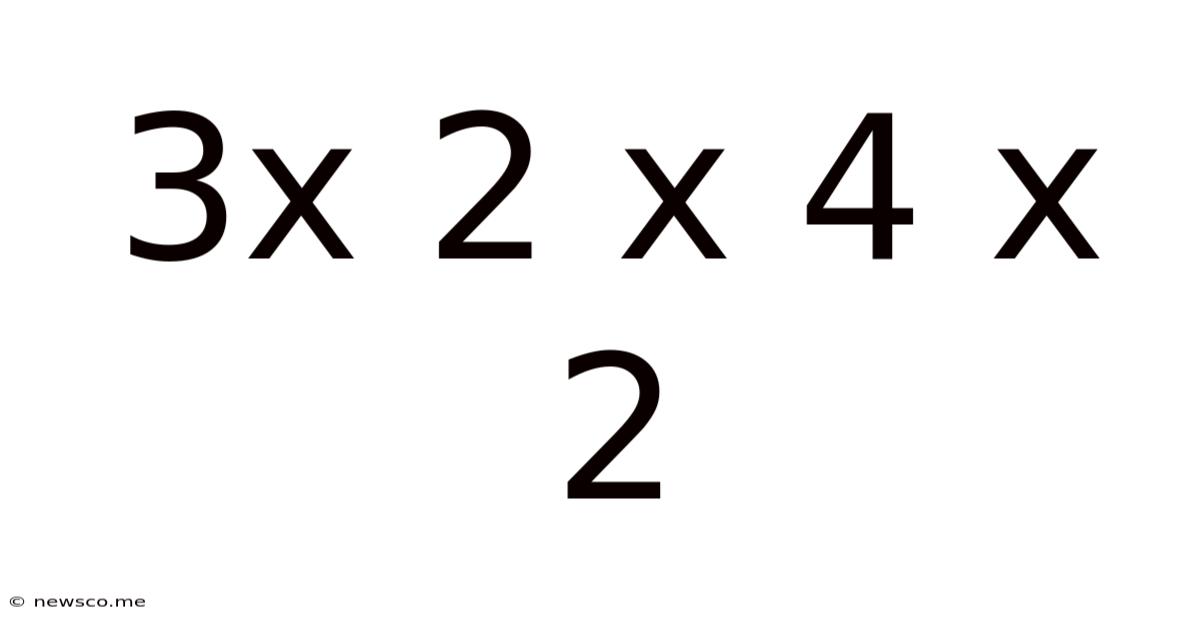
Table of Contents
Decoding 3 x 2 x 4 x 2: A Deep Dive into Multiplication and its Applications
The seemingly simple expression "3 x 2 x 4 x 2" offers a surprisingly rich opportunity to explore the fundamentals of multiplication, its various applications in diverse fields, and even delve into some advanced mathematical concepts. This article aims to provide a comprehensive analysis of this expression, going beyond a simple numerical answer to illuminate its underlying significance.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is a concise way of representing repeated addition. 3 x 2, for instance, is the same as 2 + 2 + 2, resulting in 6. This foundational understanding is crucial for grasping more complex multiplications. In our expression, 3 x 2 x 4 x 2 can be broken down into a series of repeated additions:
- 3 x 2: 2 + 2 + 2 = 6
- 6 x 4: 4 + 4 + 4 + 4 + 4 + 4 = 24
- 24 x 2: 24 + 24 = 48
Therefore, the answer to 3 x 2 x 4 x 2 is 48. However, understanding the process is just as important, if not more so, than obtaining the final result.
The Commutative Property and its Implications
Multiplication possesses a crucial property called the commutative property, which states that the order of the numbers being multiplied does not affect the final product. This means that 3 x 2 x 4 x 2 is equivalent to 2 x 4 x 3 x 2, or any other permutation of these numbers. This flexibility is highly valuable in simplifying calculations and choosing the most efficient method for solving a problem. For example, noticing that 2 x 2 = 4 allows us to simplify the calculation:
(3 x 2) x (4 x 2) = 6 x 8 = 48
This illustrates the strategic use of the commutative property to streamline the calculation.
The Associative Property: Grouping for Efficiency
The associative property of multiplication further enhances our ability to manipulate expressions. This property states that the grouping of numbers in a multiplication does not affect the final product. We can group the numbers in any way we choose, for example:
- (3 x 2) x (4 x 2) = 6 x 8 = 48
- (3 x 2 x 4) x 2 = 24 x 2 = 48
- 3 x (2 x 4 x 2) = 3 x 16 = 48
This property allows for flexibility in choosing the most convenient grouping depending on the context and the numbers involved. This is especially helpful when dealing with larger or more complex expressions.
Applications in Real-World Scenarios
The simplicity of "3 x 2 x 4 x 2" belies its widespread applicability across diverse fields:
-
Geometry: Imagine calculating the volume of a rectangular prism. If the prism has dimensions of 3 units, 2 units, and 4 units, the volume is simply 3 x 2 x 4 = 24 cubic units. Multiplying this by 2 could represent two identical prisms stacked on top of each other, leading to a total volume of 48 cubic units.
-
Business and Finance: Calculating total earnings from selling multiple items is a common application. If you sell 3 items at $2 each, 4 items at $2 each, and then double the total sales, you would use the calculation 3 x 2 x 4 x 2 to arrive at the total earnings of $48.
-
Computer Science: In programming and data structures, multiplication is integral to array indexing, memory allocation, and various algorithm complexities. Understanding the fundamental principles of multiplication ensures efficient code development and optimization.
-
Everyday Life: Many everyday tasks involve multiplication, such as calculating the total cost of groceries, determining the number of tiles needed for a floor, or even planning a party with multiple guests and items per guest.
Extending the Concept: Beyond Basic Multiplication
While seemingly straightforward, "3 x 2 x 4 x 2" can serve as a springboard to explore more advanced mathematical concepts:
-
Exponents: We can rewrite the expression using exponents. Since 2 x 2 = 2², the expression becomes 3 x 2² x 4 x 1, demonstrating the relationship between multiplication and exponents.
-
Factorials: While not directly applicable here, understanding factorials (the product of all positive integers up to a given number) is an essential concept in combinatorics and probability.
-
Matrices: In linear algebra, matrix multiplication involves a more complex form of multiplication, extending the fundamental concept to arrays of numbers. Understanding basic multiplication is foundational to grasping matrix multiplication.
-
Algebra: Introducing variables, the expression could become a x b x c x d, where a, b, c, and d represent any numbers. This transition into algebraic expressions demonstrates the power of generalization and abstraction in mathematics.
Improving Calculation Efficiency: Mental Math Techniques
Developing mental math skills significantly enhances mathematical proficiency and problem-solving speed. For our expression, several techniques can streamline calculations:
-
Prioritize simple multiplications: Immediately recognizing that 2 x 2 = 4 simplifies the calculation.
-
Group numbers strategically: The associative property allows grouping for easier mental calculation, such as (3 x 2) x (4 x 2) = 6 x 8 = 48.
-
Use doubling and halving: Doubling one number and halving another often simplifies calculations.
Conclusion: The Unsung Power of Simple Multiplication
The expression 3 x 2 x 4 x 2, though seemingly simple, provides a rich platform for exploring core mathematical principles, enhancing computational skills, and appreciating the widespread applicability of multiplication across numerous fields. Understanding the commutative and associative properties, mastering mental math techniques, and connecting this simple expression to more advanced mathematical concepts opens doors to a deeper understanding of mathematics and its crucial role in problem-solving and real-world applications. This seemingly insignificant equation reveals the powerful beauty and hidden complexities within even the most basic arithmetic operations, illustrating the importance of understanding the "why" behind the "how" in mathematics. The journey from simply calculating the answer (48) to understanding the underlying principles and their applications is far more rewarding and crucial for developing strong mathematical intuition and skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3x 2 X 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.