4.5 Divided By Sin 42 Degrees
News Co
Mar 28, 2025 · 5 min read
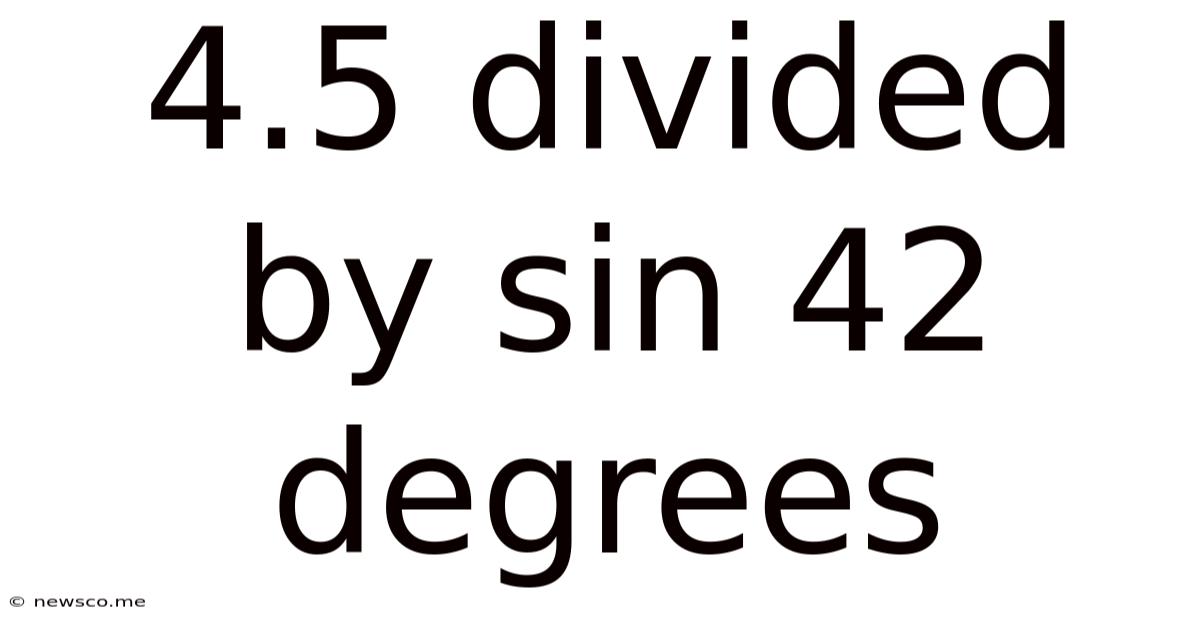
Table of Contents
4.5 Divided by Sin 42 Degrees: A Deep Dive into Trigonometric Calculations
This article delves into the seemingly simple calculation of 4.5 divided by the sine of 42 degrees (4.5/sin(42°)). While the calculation itself is straightforward using a calculator, understanding the underlying trigonometric principles and potential applications provides a richer understanding of mathematics and its practical uses. We'll explore the solution, discuss the significance of sine in trigonometry, examine potential real-world applications, and address common pitfalls and considerations in such calculations.
Understanding the Sine Function
Before diving into the calculation, it's crucial to grasp the concept of the sine function within the framework of trigonometry. The sine function, denoted as sin(θ), is one of the three primary trigonometric functions (along with cosine and tangent). It describes the ratio of the length of the side opposite an angle (θ) in a right-angled triangle to the length of the hypotenuse.
The Right-Angled Triangle
The sine function is inherently linked to right-angled triangles. In a right-angled triangle, the hypotenuse is the longest side, opposite the right angle (90°). The sine of an acute angle (θ) in this triangle is defined as:
sin(θ) = Opposite side / Hypotenuse
Beyond Right-Angled Triangles
While the sine function's definition originates from right-angled triangles, its application extends far beyond this geometric constraint. Through the concept of the unit circle, sine can be defined for any angle, even those greater than 90°. This expanded definition is crucial for understanding its use in various fields.
Calculating 4.5 / sin(42°)
Now, let's tackle the calculation: 4.5 divided by the sine of 42 degrees. This requires a calculator capable of handling trigonometric functions. Most scientific calculators and many applications (such as those found on smartphones and computers) include this functionality.
Steps:
-
Find the sine of 42°: Using your calculator, input "sin(42°)" (ensure your calculator is set to degrees, not radians). You should obtain a value close to 0.6691.
-
Perform the division: Divide 4.5 by the value obtained in step 1. Therefore, 4.5 / 0.6691 ≈ 6.725
Therefore, 4.5 divided by sin(42°) is approximately 6.725. The precision depends on the number of decimal places your calculator uses.
Real-World Applications: Where is this Calculation Useful?
This seemingly simple calculation has surprising real-world applicability in diverse fields. Here are a few examples:
1. Physics and Engineering: Determining Forces and Vectors
In physics and engineering, calculations involving angles and forces are commonplace. Imagine a scenario where a force of 4.5 Newtons is applied at an angle of 42° to a surface. The component of the force acting perpendicular to the surface (which could be crucial for determining friction or pressure) can be calculated using the sine function:
- Perpendicular force component = 4.5 * sin(42°)
- Then, 4.5 / sin(42°) would provide a related calculation for solving other variables within the problem
2. Surveying and Navigation: Determining Distances and Heights
Surveyors and navigators use trigonometry extensively. Consider a situation where a surveyor needs to determine the height of a building. By measuring the distance to the building and the angle of elevation from the ground, the height can be calculated using the sine function. This involves similar calculations involving the sine function and therefore the principles behind this calculation are relevant.
3. Computer Graphics and Game Development: Creating Realistic Scenes
In computer graphics and game development, trigonometric functions are fundamental for creating realistic 3D environments. The calculation of lighting, shadows, and object placement often relies on trigonometric relationships. Again, the principles explored here are foundational to these more complex calculations.
4. Astronomy and Astrophysics: Studying Celestial Objects
Calculations involving celestial positions and distances often leverage trigonometric functions, particularly the sine function. For instance, determining the distance to a star involves using angles and distances, leading to similar mathematical operations involving sines and other trigonometric functions.
Potential Pitfalls and Considerations
While the calculation is straightforward, several points merit attention:
-
Units: Ensure your calculator is set to degrees (°) and not radians. Radians are another unit of angular measurement, and using the wrong unit will result in an incorrect answer.
-
Significant Figures: The number of significant figures in your answer should reflect the precision of your input values. If 4.5 is measured to only one decimal place, the result should not be presented with excessive precision.
-
Calculator Accuracy: Calculators have limitations in their precision. Very small or very large numbers might lead to rounding errors, especially when dealing with complex calculations involving multiple trigonometric functions.
-
Inverse Sine Function: The inverse sine function (arcsin or sin⁻¹) is crucial for finding angles when you know the ratio of sides in a right-angled triangle. Understanding this inverse relationship complements the knowledge of the basic sine function.
Conclusion: Expanding Your Mathematical Horizons
The seemingly simple calculation of 4.5 / sin(42°) serves as a gateway to understanding the broader applications of trigonometry in various scientific and engineering disciplines. While a calculator readily provides the numerical answer, grasping the underlying principles—the definition of the sine function, its relationship to right-angled triangles, and its extensions beyond simple geometry—enhances mathematical comprehension and practical problem-solving skills. Furthermore, recognizing the potential for application in diverse fields highlights the importance of mastering fundamental mathematical concepts for tackling more complex challenges. By understanding these principles, you can confidently apply similar calculations to a variety of real-world problems and further expand your mathematical knowledge. Further exploration into related trigonometric functions such as cosine and tangent will provide even greater depth and understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about 4.5 Divided By Sin 42 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.