4 D 7 G 10 J 13
News Co
Mar 31, 2025 · 5 min read
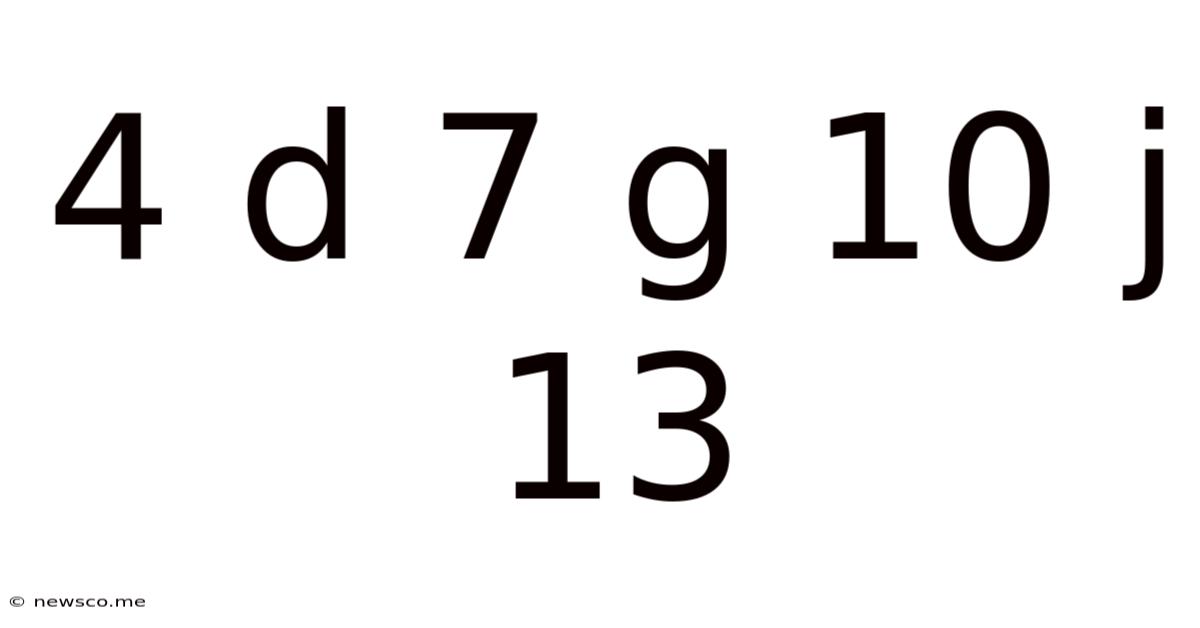
Table of Contents
Decoding the Sequence: 4D 7G 10J 13... and the Secrets of Number Patterns
The seemingly simple sequence "4D 7G 10J 13..." might appear innocuous at first glance. However, beneath its unassuming exterior lies a fascinating puzzle involving number patterns, letter sequences, and the intriguing interplay between arithmetic and alphabetic systems. This article delves deep into the logic behind this sequence, exploring its underlying structure, potential extensions, and its relevance to broader mathematical and cryptographic concepts.
Unveiling the Pattern: Numbers and Letters
The core of this sequence lies in its dual nature: a numerical progression intertwined with an alphabetical one. Let's break it down:
-
Numerical Progression: The numbers – 4, 7, 10, 13 – form an arithmetic sequence. Each subsequent number is obtained by adding 3 to the previous one. This is a fundamental concept in arithmetic and forms the bedrock of our sequence.
-
Alphabetical Progression: The letters – D, G, J, – represent a different kind of progression. They are not consecutive letters of the alphabet, but rather, each letter is three positions ahead of the previous one. D is three positions after A, G is three positions after D, and J is three positions after G.
This reveals a beautifully symmetrical structure: a constant difference of 3 governs both the numerical and alphabetical parts of the sequence.
Extending the Sequence: Predicting the Future
Understanding the underlying pattern allows us to predict the continuation of the sequence. Following the established rule, the next terms would be:
- 16M: 13 + 3 = 16, and J + 3 positions = M
- 19P: 16 + 3 = 19, and M + 3 positions = P
- 22R: 19 + 3 = 22, and P + 3 positions = R
- 25U: 22 + 3 = 25, and R + 3 positions = U
- 28X: 25 + 3 = 28, and U + 3 positions = X
- 31A: 28 + 3 = 31, and X + 3 positions = A (The alphabet cycles back to A)
This demonstrates the elegance and predictability inherent in the sequence. The consistent application of the +3 rule ensures a clear and logical progression.
Deeper Dive: Mathematical Concepts in Play
The sequence's simplicity belies its connection to more sophisticated mathematical ideas:
Arithmetic Sequences and Series:
At its heart, the numerical part of the sequence is a classic example of an arithmetic sequence. These sequences are characterized by a constant difference between consecutive terms (in this case, 3). Understanding arithmetic sequences is crucial in various fields, including:
- Financial Mathematics: Calculating compound interest, loan repayments, and future value of investments.
- Physics: Modeling uniformly accelerated motion.
- Computer Science: Analyzing algorithms and data structures.
Modular Arithmetic:
The alphabetical portion of the sequence subtly introduces the concept of modular arithmetic. When the letter progression reaches the end of the alphabet (Z), it wraps around back to A. This cyclical behavior is analogous to modular arithmetic, where numbers "wrap around" after reaching a certain modulus (in this case, 26, the number of letters in the alphabet). Modular arithmetic is fundamental to:
- Cryptography: Ensuring secure communication and data encryption.
- Computer Science: Handling data structures and algorithms efficiently.
- Number Theory: Exploring the properties of integers and their relationships.
Mapping Functions:
We can consider this sequence as a demonstration of a simple mapping function. This function takes a numerical input (n) and maps it to an ordered pair (n, L), where L is the letter corresponding to the alphabetical progression. The function could be expressed (informally) as:
f(n) = (n, L), where n = 4 + 3k, and L is the kth letter in the sequence starting from D.
This formalization highlights the mathematical precision and structure underlying the apparently random sequence.
Beyond the Sequence: Applications and Implications
While seemingly a simple puzzle, the "4D 7G 10J 13..." sequence holds relevance in various contexts:
Cryptography and Code-Breaking:
Sequences like this, with their intricate patterns, serve as building blocks for more complex cryptographic systems. The underlying principles of modular arithmetic and number theory are central to modern encryption techniques. Analyzing and deciphering such patterns is a crucial skill in cryptography and code-breaking.
Algorithmic Thinking and Problem Solving:
Understanding the sequence encourages the development of algorithmic thinking. To extend or manipulate the sequence requires breaking down the problem into logical steps and applying consistent rules. This approach to problem-solving is valuable in various fields, including computer science, engineering, and even everyday life.
Educational Tool:
This sequence can serve as an engaging and accessible educational tool for teaching fundamental mathematical concepts to students at different levels. It visually demonstrates arithmetic progressions, modular arithmetic, and the relationship between numerical and alphabetical systems in a relatable and easy-to-understand way.
Expanding Horizons: Variations and Further Exploration
The basic sequence can be modified and expanded to explore a multitude of possibilities:
- Changing the Common Difference: Instead of adding 3, we could add any integer, altering both the numerical and alphabetical progressions.
- Different Starting Points: Changing the initial number (4) and letter (D) would generate different sequences.
- Non-linear Progressions: Instead of an arithmetic sequence, we could explore geometric progressions or other more complex numerical patterns.
- Multiple Alphabets: The sequence could be expanded to use multiple alphabets or other symbol sets.
These variations offer endless opportunities for exploration and the discovery of even more complex and interesting patterns.
Conclusion: A Simple Sequence with Profound Implications
The "4D 7G 10J 13..." sequence, though deceptively simple, provides a gateway to explore fundamental mathematical concepts, algorithmic thinking, and the intriguing interplay between numbers and letters. Its underlying structure demonstrates the power of patterns and the beauty of mathematical symmetry. Whether viewed as a mathematical puzzle, a cryptographic precursor, or an educational tool, this sequence offers a compelling example of how seemingly simple ideas can reveal deep connections within the world of mathematics. Further exploration of its variations and generalizations promises to unlock even more intricate and fascinating discoveries, showcasing the richness and depth hidden within even the most basic of number sequences.
Latest Posts
Related Post
Thank you for visiting our website which covers about 4 D 7 G 10 J 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.