4 Divided By 1/6 In Fraction Form
News Co
May 08, 2025 · 5 min read
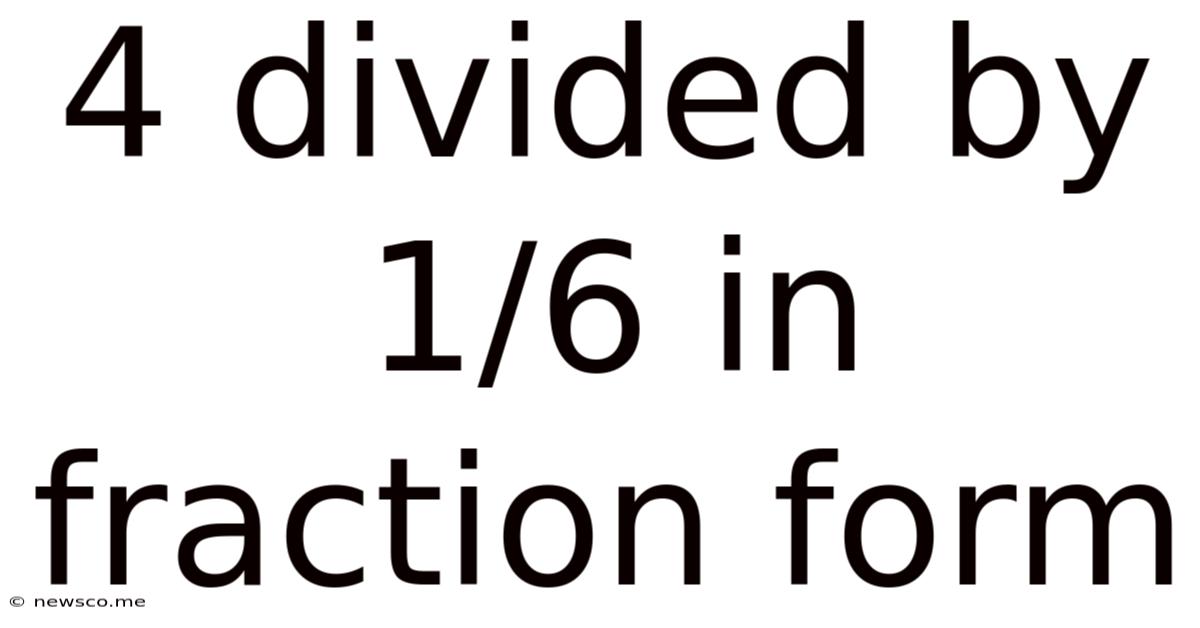
Table of Contents
4 Divided by 1/6 in Fraction Form: A Comprehensive Guide
Understanding fractions and how to perform operations with them is a cornerstone of mathematics. This guide will delve deep into the seemingly simple problem of 4 divided by 1/6, explaining the process in detail, exploring different approaches, and providing a solid foundation for tackling similar fraction division problems. We'll go beyond the simple answer and explore the underlying concepts, making sure you understand why the solution works the way it does.
Understanding the Problem: 4 ÷ 1/6
The question, "What is 4 divided by 1/6?" might seem straightforward at first glance. However, dividing by a fraction introduces a crucial concept that often trips up learners: reciprocals.
What is a Reciprocal?
A reciprocal, also known as a multiplicative inverse, is the number that, when multiplied by the original number, results in 1. To find the reciprocal of a fraction, simply switch the numerator and the denominator.
For example:
- The reciprocal of 1/6 is 6/1 (or simply 6).
- The reciprocal of 3/4 is 4/3.
- The reciprocal of 5 is 1/5 (because 5 can be written as 5/1).
This concept of reciprocals is central to dividing fractions.
Method 1: The "Keep, Change, Flip" Method
This popular method provides a straightforward way to divide fractions:
-
Keep: Keep the first number (the dividend) as it is. In our case, this is 4. We can express 4 as the fraction 4/1.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (find the reciprocal of) the second number (the divisor). The reciprocal of 1/6 is 6/1 (or 6).
Therefore, 4 ÷ 1/6 becomes:
4/1 × 6/1
Now, we simply multiply the numerators together and the denominators together:
(4 × 6) / (1 × 1) = 24/1 = 24
Therefore, 4 divided by 1/6 is 24.
Visualizing the Solution
Imagine you have 4 pizzas, and you want to divide each pizza into sixths (1/6). How many slices (1/6 of a pizza) do you have in total? You'd have 4 pizzas x 6 slices/pizza = 24 slices. This visual representation reinforces the mathematical solution.
Method 2: Using the Definition of Division
Division can be defined as the inverse operation of multiplication. This means that a ÷ b is equivalent to finding a number 'x' such that b × x = a.
In our case:
1/6 × x = 4
To solve for 'x', we can multiply both sides of the equation by the reciprocal of 1/6 (which is 6):
6 × (1/6 × x) = 6 × 4
This simplifies to:
x = 24
Again, we arrive at the solution: 24. This method showcases the relationship between division and multiplication in a more formal mathematical context.
Method 3: Converting to Decimal Form (Less Preferred for Accuracy)
While less accurate for some fraction problems, especially those involving repeating decimals, converting to decimal form can be a helpful supplementary approach for some.
- Convert 1/6 to a decimal: 1/6 ≈ 0.166666... (a repeating decimal)
- Divide 4 by the decimal approximation: 4 ÷ 0.166666... ≈ 24
Note: Due to the repeating decimal, this method may introduce slight inaccuracies depending on the level of decimal precision used. Therefore, the fraction method is always preferred for its exactness.
Expanding the Understanding: Different Types of Fraction Division Problems
The principles illustrated above can be applied to a wider range of fraction division problems. Let's explore some examples:
Example 1: A Fraction Divided by a Fraction
Let's say we want to solve 2/3 ÷ 1/4. Applying the "Keep, Change, Flip" method:
2/3 ÷ 1/4 = 2/3 × 4/1 = 8/3
This simplifies to the mixed number 2 2/3.
Example 2: A Mixed Number Divided by a Fraction
Suppose we need to solve 1 1/2 ÷ 2/5. First, convert the mixed number to an improper fraction: 1 1/2 = 3/2. Then apply the "Keep, Change, Flip" method:
3/2 ÷ 2/5 = 3/2 × 5/2 = 15/4
This simplifies to the mixed number 3 3/4.
Common Mistakes to Avoid
Many students struggle with fraction division, often making these common mistakes:
- Forgetting to find the reciprocal: Simply multiplying the two fractions without flipping the second one will lead to an incorrect answer.
- Incorrectly multiplying or simplifying fractions: Remember the rules of fraction multiplication: multiply numerators and denominators separately, then simplify the resulting fraction.
- Not converting mixed numbers to improper fractions: Before dividing, always convert mixed numbers into improper fractions to make the calculation easier and avoid errors.
Practice Makes Perfect
The best way to master fraction division is through practice. Try solving various problems, ranging from simple to complex, using different methods. This will solidify your understanding and build your confidence.
Conclusion: Mastering Fraction Division
Understanding fraction division, especially problems like 4 divided by 1/6, is crucial for building a solid mathematical foundation. The "Keep, Change, Flip" method offers a simple and efficient approach, while understanding the underlying concept of reciprocals and the definition of division provides a deeper appreciation of the process. By mastering these concepts and practicing regularly, you can confidently tackle any fraction division problem you encounter. Remember, the key is to be systematic and to check your work to ensure accuracy. Through consistent effort, you will build your proficiency and gain a strong command of this essential mathematical skill.
Latest Posts
Latest Posts
-
Are The Two Indicated Angles Adjacent Why Or Why Not
May 09, 2025
-
The Longest Side Of A Right Triangle Is Called The
May 09, 2025
-
Find X Round To The Nearest Tenth Of A Degree
May 09, 2025
-
How Many Edges Does Cylinder Have
May 09, 2025
-
Which Of The Following Is A Discrete Random Variable
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 1/6 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.