4 Divided By 6 As A Fraction
News Co
Mar 15, 2025 · 5 min read
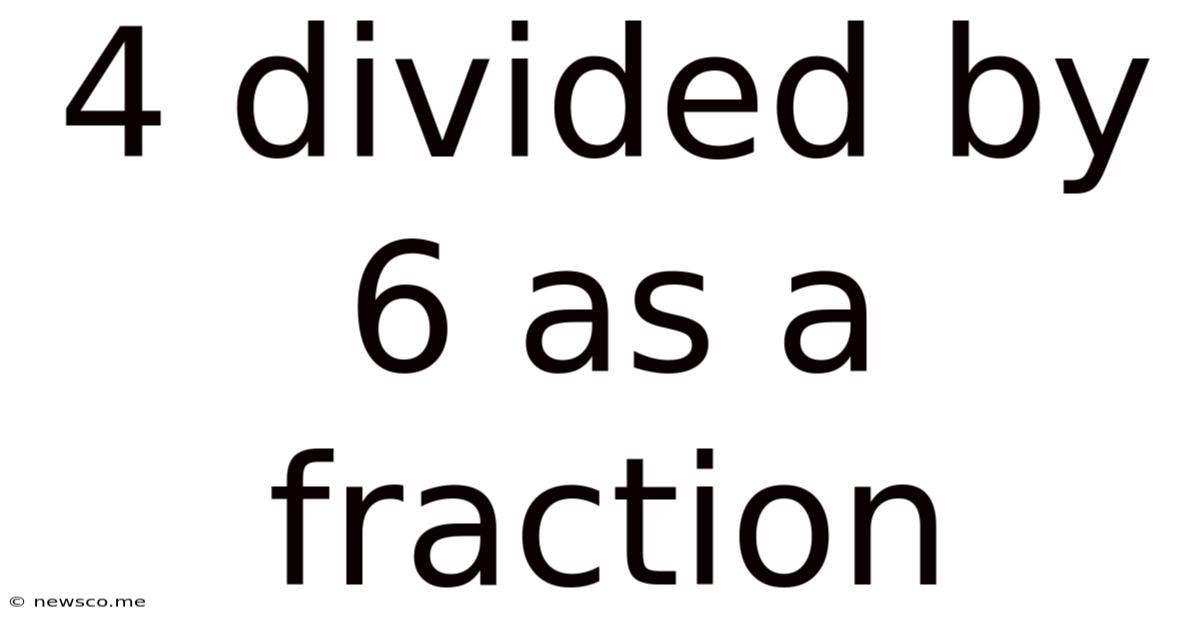
Table of Contents
4 Divided by 6 as a Fraction: A Comprehensive Guide
Understanding fractions is fundamental to mathematics, and expressing division as a fraction is a key concept. This comprehensive guide delves into the process of representing 4 divided by 6 as a fraction, exploring the underlying principles and offering practical applications. We'll cover simplifying fractions, converting fractions to decimals, and exploring real-world examples to solidify your understanding.
Understanding the Fundamentals: Division and Fractions
Before diving into the specific problem of 4 divided by 6, let's establish a solid foundation. Division and fractions are intrinsically linked. When we divide one number (the dividend) by another (the divisor), the result can be expressed as a fraction. The dividend becomes the numerator (top number), and the divisor becomes the denominator (bottom number).
In essence, the division problem "a ÷ b" is equivalent to the fraction a/b.
This is a crucial understanding because it provides a powerful tool for representing division problems in a concise and readily understandable format.
Expressing 4 Divided by 6 as a Fraction
Now, let's tackle our specific problem: 4 divided by 6. Using the principle outlined above, we can directly represent this as a fraction:
4 ÷ 6 = 4/6
This fraction, 4/6, represents the result of dividing 4 by 6. However, this fraction isn't in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator.
Simplifying Fractions: Finding the Greatest Common Divisor (GCD)
The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Finding the GCD allows us to reduce the fraction to its simplest form, making it easier to understand and work with.
Several methods exist for finding the GCD. Let's explore two common approaches:
1. Listing Factors:
This method involves listing all the factors of both the numerator and denominator and identifying the largest common factor.
- Factors of 4: 1, 2, 4
- Factors of 6: 1, 2, 3, 6
The largest common factor is 2.
2. Prime Factorization:
This method involves breaking down both the numerator and denominator into their prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 6: 2 x 3
The common prime factor is 2, and the lowest power is 2¹. Therefore, the GCD is 2.
Simplifying 4/6 to its Lowest Terms
Now that we've identified the GCD as 2, we can simplify the fraction 4/6 by dividing both the numerator and denominator by 2:
4/6 = (4 ÷ 2) / (6 ÷ 2) = 2/3
Therefore, the simplified fraction representing 4 divided by 6 is 2/3. This is the most concise and accurate way to express the result of this division.
Converting Fractions to Decimals
While fractions are useful, sometimes it's helpful to represent the result as a decimal. To convert a fraction to a decimal, simply divide the numerator by the denominator:
2 ÷ 3 = 0.666...
The result is a recurring decimal, meaning the digit 6 repeats infinitely. This can be represented as 0.6̅ or 0.666… This decimal representation provides another way to understand the value of 4 divided by 6.
Real-World Applications: Understanding Fractions in Context
Understanding fractions and their relationship to division is crucial in various real-world scenarios. Let's consider a few examples:
Example 1: Sharing Pizza
Imagine you have 4 slices of pizza and you want to share them equally among 6 people. Each person gets 4/6 of a pizza slice, which simplifies to 2/3 of a slice.
Example 2: Calculating Proportions
In cooking, you might need to adjust a recipe. If a recipe calls for 6 cups of flour, but you only want to make 4/6 of the recipe, you would need to use (4/6) * 6 cups = 4 cups of flour.
Example 3: Measuring Lengths
Imagine a project requiring a piece of wood 6 meters long, and you only need 4 meters. You're using 4/6 or 2/3 of the total length.
These examples demonstrate that fractions are not merely abstract mathematical concepts but practical tools for solving everyday problems involving division and proportions.
Advanced Concepts: Improper Fractions and Mixed Numbers
While 4/6 is a proper fraction (numerator < denominator), understanding improper fractions (numerator ≥ denominator) and mixed numbers (a whole number and a proper fraction) is crucial for a comprehensive understanding of fractions.
If we had a problem like 6 divided by 4, we would get 6/4, an improper fraction. This can be converted to a mixed number by dividing the numerator by the denominator:
6 ÷ 4 = 1 with a remainder of 2. This can be expressed as 1 2/4, which simplifies to 1 ½.
Conclusion: Mastering Fractions for a Strong Mathematical Foundation
This comprehensive guide provides a thorough understanding of representing 4 divided by 6 as a fraction. We explored the core principles of division and fractions, simplified fractions using GCD, converted fractions to decimals, and applied these concepts to practical real-world scenarios. Mastering these foundational concepts is crucial for success in further mathematical studies and everyday problem-solving. The ability to confidently work with fractions, understand their relationship to division, and convert between fractions and decimals opens doors to a deeper understanding of mathematical concepts and their applications in various fields. Remember that consistent practice is key to solidifying your understanding and developing proficiency in working with fractions. By actively engaging with these concepts and applying them to diverse problems, you'll build a strong and lasting foundation in mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about 4 Divided By 6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.