4 Divided By 9 As A Fraction
News Co
Mar 28, 2025 · 5 min read
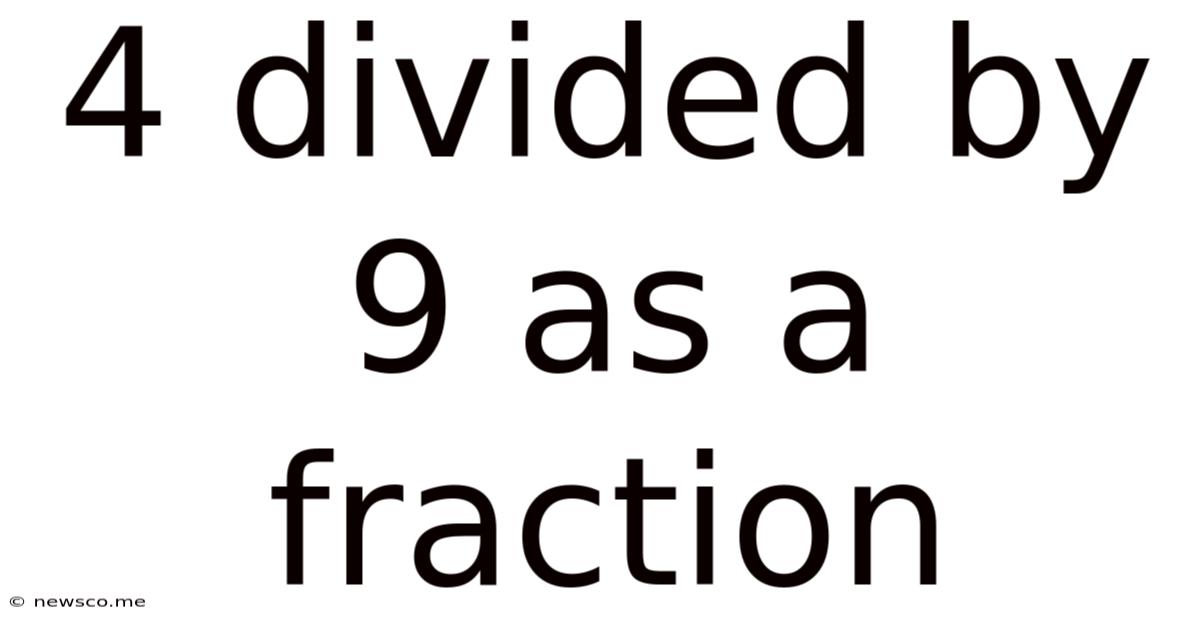
Table of Contents
4 Divided by 9 as a Fraction: A Comprehensive Guide
Understanding fractions is a fundamental concept in mathematics, forming the bedrock for more advanced topics. This comprehensive guide will delve into the seemingly simple yet crucial operation of dividing 4 by 9 and expressing the result as a fraction. We'll explore different methods, address common misconceptions, and highlight the practical applications of this seemingly basic calculation.
Understanding Division and Fractions
Before diving into the specific calculation, let's review the core concepts. Division is essentially the process of splitting a quantity into equal parts. A fraction, on the other hand, represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into.
For instance, the fraction ½ represents one part out of two equal parts. Similarly, ⅘ represents four parts out of five equal parts.
Expressing 4 Divided by 9 as a Fraction
The question "4 divided by 9" can be written mathematically as 4 ÷ 9. To express this as a fraction, we simply write the dividend (the number being divided, 4) as the numerator and the divisor (the number we're dividing by, 9) as the denominator. Therefore, 4 divided by 9 as a fraction is ⁴⁄₉.
This fraction is already in its simplest form because 4 and 9 share no common factors other than 1. A fraction is in its simplest form when the numerator and denominator have no common divisors greater than 1 (i.e., they are co-prime).
Alternative Methods and Representations
While writing the fraction directly is the simplest method, let's explore alternative approaches to reinforce the understanding:
Using Long Division
Long division provides a different perspective on the division process. When we divide 4 by 9, we get a decimal result: 0.444... (a repeating decimal). This repeating decimal, 0.4̅, is another way of representing ⁴⁄₉. This highlights the connection between fractions and decimals.
Visual Representation
Visual aids can significantly improve comprehension, especially for beginners. Imagine a pizza cut into nine equal slices. If you have four slices, you possess ⁴⁄₉ of the pizza. This visual representation directly connects the abstract concept of a fraction to a tangible example.
Common Misconceptions and Errors
Several common misconceptions can hinder the understanding of fractions and division:
-
Reversing the Numerator and Denominator: A frequent error is reversing the numerator and denominator. Remember, the dividend (the number being divided) always forms the numerator, and the divisor (the number dividing) forms the denominator. ⁹⁄₄ is incorrect.
-
Incorrect Simplification: Always ensure the fraction is simplified to its lowest terms. For instance, if the result were ⁸⁄₁₈, it should be simplified to ⁴⁄₉ by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 2.
-
Confusing Division with Multiplication: Division and multiplication are inverse operations. Don't confuse the process of division with multiplication, which would result in a completely different answer.
Practical Applications of ⁴⁄₉
Understanding fractions isn't just an academic exercise; it has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Understanding fractions is crucial for accurate measurements and successful cooking.
-
Construction and Engineering: Accurate measurements and calculations using fractions are essential in construction and engineering projects to ensure structural integrity and functionality.
-
Finance and Budgeting: Fractions are used extensively in financial calculations, such as calculating percentages, interest rates, and proportions of budgets.
-
Data Analysis and Statistics: Fractions and decimals (which are related to fractions) are frequently used to represent proportions and probabilities in data analysis and statistics.
Expanding on Fractions: Further Exploration
Understanding ⁴⁄₉ as a fraction lays the foundation for more complex fractional operations:
-
Adding and Subtracting Fractions: To add or subtract fractions, you need a common denominator. For example, adding ⁴⁄₉ + ²/₉ is straightforward (⁶⁄₉ which simplifies to ²⁄₃). However, adding fractions with different denominators requires finding a least common multiple (LCM) to obtain a common denominator.
-
Multiplying Fractions: Multiplying fractions involves multiplying the numerators and multiplying the denominators separately. For instance, ⁴⁄₉ x ²⁄₃ = ⁸⁄₂₇.
-
Dividing Fractions: Dividing fractions involves inverting the second fraction (the divisor) and then multiplying. For example, ⁴⁄₉ ÷ ²⁄₃ = ⁴⁄₉ x ³⁄₂ = ¹²/₁₈ = ²⁄₃.
-
Converting Fractions to Decimals and Percentages: As mentioned earlier, ⁴⁄₉ can be converted to a repeating decimal (0.4̅) and then to a percentage (approximately 44.44%). These conversions are essential for understanding the magnitude and relative size of fractions in different contexts.
-
Working with Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 2 ¾). Converting mixed numbers to improper fractions (where the numerator is larger than the denominator) is often required for calculations involving fractions.
-
Solving Equations with Fractions: Fractions appear in many algebraic equations. Understanding how to manipulate fractions in equations is critical for solving them correctly.
Conclusion: Mastering Fractions for a Broader Mathematical Understanding
The seemingly simple operation of dividing 4 by 9 and expressing it as the fraction ⁴⁄₉ opens up a world of mathematical possibilities. This guide has not only provided the answer but also explored the underlying principles, addressed common misconceptions, and highlighted the practical relevance of fractions in various fields. Mastering fractions is crucial not only for academic success but also for navigating the quantitative aspects of everyday life. By understanding the concepts explained here, you'll build a strong foundation for more complex mathematical concepts and problem-solving in the future. The seemingly basic ⁴⁄₉ is a stepping stone to a deeper appreciation of the power and versatility of fractions.
Latest Posts
Related Post
Thank you for visiting our website which covers about 4 Divided By 9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.