4 + X + 3 + 2x And 10x
News Co
May 09, 2025 · 5 min read
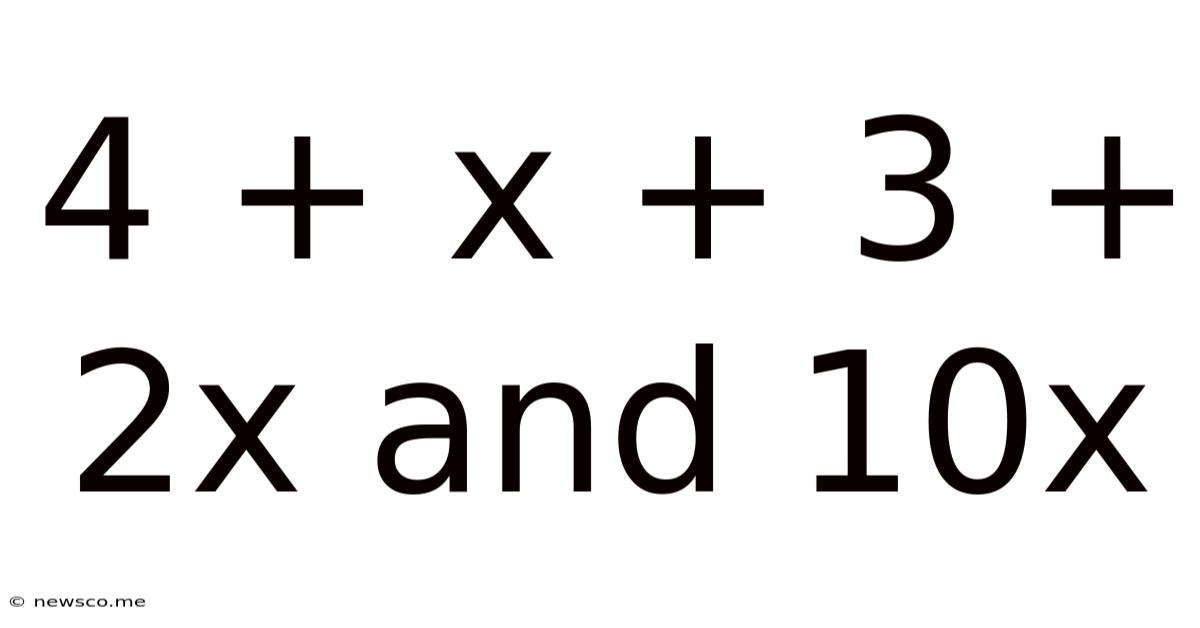
Table of Contents
Unveiling the Mysteries of Algebraic Expressions: A Deep Dive into 4 + x + 3 + 2x and 10x
This article delves into the fascinating world of algebra, focusing specifically on the expressions 4 + x + 3 + 2x and 10x. We'll explore simplification, equivalence, solutions, and the broader applications of these seemingly simple expressions. Understanding these fundamentals is crucial for anyone venturing into the realm of mathematics, from students grappling with elementary algebra to professionals using mathematical models in their fields.
Understanding the Building Blocks: Variables and Constants
Before we dissect our expressions, let's clarify some fundamental algebraic concepts. An algebraic expression is a combination of variables, constants, and mathematical operations (addition, subtraction, multiplication, division).
-
Variables: These are represented by letters (like 'x' in our examples) and represent unknown quantities or values that can change.
-
Constants: These are fixed numerical values (like 4 and 3 in our expressions). They don't change.
Our expressions, 4 + x + 3 + 2x and 10x, perfectly illustrate this. 'x' is the variable, while 4 and 3 are constants.
Simplifying 4 + x + 3 + 2x
The expression 4 + x + 3 + 2x can be simplified by combining like terms. Like terms are terms that have the same variable raised to the same power. In our case, 'x' and '2x' are like terms, and 4 and 3 are like terms.
Here's how we simplify:
-
Combine constant terms: 4 + 3 = 7
-
Combine 'x' terms: x + 2x = 3x
Therefore, the simplified expression is 7 + 3x. This is equivalent to the original expression; it just represents it in a more concise and manageable form.
Exploring the Relationship between 7 + 3x and 10x
The expressions 7 + 3x and 10x are not equivalent. They represent different mathematical relationships. They will only be equal under specific circumstances, which we'll explore later when discussing solutions.
The expression 10x is a simple linear expression. Its value directly depends on the value of 'x'. If x doubles, the value of 10x doubles. This demonstrates a direct proportionality.
The expression 7 + 3x, however, represents a linear equation with a y-intercept. The value is influenced not only by 'x' but also by the constant term, 7. Even when x=0, the expression has a value of 7. This is because 7 represents the y-intercept in graphical representation.
Solving for x: Finding the Point of Equivalence
While 7 + 3x and 10x are generally not equal, we can find specific values of 'x' where they are. This involves solving an equation:
7 + 3x = 10x
To solve this, we need to isolate 'x' on one side of the equation.
-
Subtract 3x from both sides: 7 = 7x
-
Divide both sides by 7: x = 1
Therefore, the expressions 7 + 3x and 10x are only equal when x = 1. For any other value of 'x', the expressions will yield different results. This illustrates that different algebraic expressions can have points of intersection and equality based on the variable's value.
Visualizing the Expressions: A Graphical Approach
Graphing these expressions can provide a powerful visual representation of their relationships. We can plot them on a Cartesian coordinate system, where the x-axis represents the value of 'x' and the y-axis represents the value of the expression.
-
10x: This is a straight line passing through the origin (0,0) with a slope of 10.
-
7 + 3x: This is also a straight line, but it intersects the y-axis at 7 (the y-intercept) and has a slope of 3.
The point where these two lines intersect represents the solution to the equation 7 + 3x = 10x; specifically, the point (1, 10). This visually confirms our earlier algebraic solution where x = 1. The graph clearly demonstrates how the values of the expressions differ for all other values of 'x'.
Real-World Applications: Where These Expressions Might Appear
Although seemingly simple, these expressions have practical applications in various fields:
-
Physics: They could model velocity (10x) and distance traveled considering initial displacement (7+3x), given x as time, to describe a situation with constant acceleration and initial position.
-
Finance: They could represent simple interest calculations or linear cost models in business, where the variable 'x' represents a certain parameter and the expressions would be used to compute profit or cost.
-
Engineering: They could be used in simple linear approximations to model physical phenomena, for example in the basic relationship between distance, speed and time.
-
Computer Science: They could form parts of algorithms and mathematical models used for data processing, simulations, and predictions.
Expanding on the Concepts: Further Exploration
This analysis only scratches the surface of the possibilities. We could extend our exploration to:
-
Quadratic Expressions: Introducing squared terms (x²) would lead to more complex relationships and solutions.
-
Systems of Equations: We could involve more than one variable, leading to systems of equations requiring more advanced methods for solution.
-
Inequalities: Instead of equalities, we could explore inequalities (e.g., 7 + 3x > 10x), which introduce a range of solutions rather than a single value.
-
Calculus: As we venture into calculus, these expressions become building blocks for calculating rates of change, areas under curves, and a host of other essential concepts.
Conclusion: The Importance of Algebraic Foundations
Mastering the simplification, solution, and interpretation of algebraic expressions like 4 + x + 3 + 2x and 10x is crucial for developing a strong foundation in mathematics and its applications. While seemingly basic, these expressions highlight fundamental concepts that underlie much more complex mathematical models used in various scientific, engineering and computational fields. Understanding the relationships between these expressions, their graphical representations, and their practical applications is key to unlocking a deeper comprehension of the mathematical world around us. Further exploration of these concepts will open doors to more advanced mathematical ideas, fostering critical thinking and problem-solving abilities.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4 + X + 3 + 2x And 10x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.