40 Is 20 Of What Number
News Co
Apr 19, 2025 · 4 min read
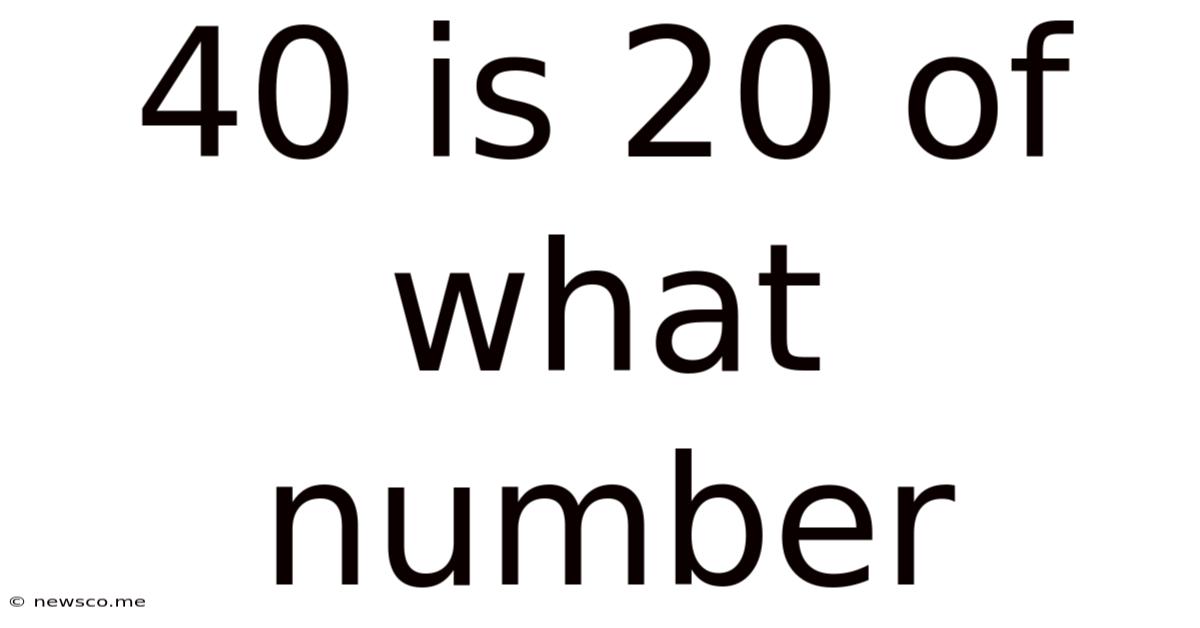
Table of Contents
40 is 20% of What Number? A Deep Dive into Percentage Calculations
Many of us encounter percentage problems in our daily lives, whether it's calculating discounts at the mall, understanding interest rates on loans, or figuring out tax percentages. One common type of percentage problem involves finding the original number when you know a percentage of it. This article will delve into how to solve the problem "40 is 20% of what number?", exploring different methods, providing step-by-step explanations, and offering practical applications. We'll also touch on the importance of understanding percentages in various contexts and explore some common pitfalls to avoid.
Understanding the Problem: Deconstructing "40 is 20% of What Number?"
The statement "40 is 20% of what number?" presents a classic percentage problem. We are given a part (40) and a percentage (20%), and our task is to find the whole (the unknown number). This type of problem frequently appears in:
- Financial calculations: Determining the original price before a discount, calculating principal amounts from interest payments, or figuring out total sales from a percentage increase.
- Statistical analysis: Interpreting survey results, analyzing data sets, and understanding proportions within larger populations.
- Everyday life: Scaling recipes, determining the total cost before tax, or calculating tips at restaurants.
Understanding these applications highlights the importance of mastering percentage calculations.
Method 1: Using the Percentage Formula
The most straightforward method to solve this problem involves using the fundamental percentage formula:
Part = Percentage × Whole
In our case:
- Part = 40
- Percentage = 20% = 0.20 (Remember to convert percentages to decimals by dividing by 100)
- Whole = x (This is the unknown number we need to find)
Substituting these values into the formula, we get:
40 = 0.20x
To solve for x (the whole), we divide both sides of the equation by 0.20:
x = 40 / 0.20
x = 200
Therefore, 40 is 20% of 200.
Method 2: Using Proportions
Another effective approach involves setting up a proportion:
Part / Whole = Percentage / 100
Again, substituting our known values:
40 / x = 20 / 100
Cross-multiplying, we obtain:
40 * 100 = 20 * x
4000 = 20x
Dividing both sides by 20:
x = 4000 / 20
x = 200
This method confirms our previous result: 40 is 20% of 200.
Method 3: Working Backwards from the Percentage
We can also think of this problem in a slightly different way. If 40 represents 20%, we can ask: what does 1% represent?
To find the value of 1%, we divide 40 by 20:
40 / 20 = 2
So, 1% of the unknown number is 2. To find the whole (100%), we multiply this value by 100:
2 * 100 = 200
Once again, we arrive at the same answer: 40 is 20% of 200.
Practical Applications: Real-World Examples
Let's explore some practical scenarios where solving this type of percentage problem is crucial:
Scenario 1: Sales Discount
A store offers a 20% discount on an item, and you save $40. What was the original price of the item?
Using the methods described above, we can determine that the original price was $200.
Scenario 2: Investment Returns
You invested some money, and your investment grew by 20%, resulting in a profit of $40. How much did you initially invest?
The initial investment was $200.
Scenario 3: Survey Results
A survey reveals that 20% of respondents prefer a particular product, and this represents 40 people. How many people participated in the survey?
A total of 200 people participated.
These examples showcase the broad applicability of solving percentage problems in various situations.
Common Mistakes to Avoid
While percentage calculations might seem straightforward, there are common pitfalls to watch out for:
- Incorrect decimal conversion: Always remember to convert percentages to decimals (divide by 100) before using them in calculations. Failing to do this leads to inaccurate results.
- Mixing up parts and wholes: Clearly identify the "part" (the given percentage amount) and the "whole" (the unknown number) to avoid confusion in setting up the equation or proportion.
- Arithmetic errors: Double-check your calculations to ensure accuracy. Even a small mistake can lead to a significant error in the final answer.
Beyond the Basics: Expanding Your Percentage Skills
Mastering the basics of percentage calculations opens the door to more complex problems. These include:
- Calculating percentage increases and decreases: Understanding how to find the percentage change between two values.
- Working with compound interest: Calculating interest earned over multiple periods, where interest is added to the principal amount.
- Solving problems involving multiple percentages: Dealing with scenarios where you need to calculate several percentages successively.
By building a solid foundation in basic percentage calculations, you'll be well-equipped to tackle these more advanced concepts.
Conclusion: The Power of Percentage Proficiency
The ability to confidently solve percentage problems like "40 is 20% of what number?" is an invaluable skill in numerous aspects of life. From managing personal finances to analyzing data and understanding the world around us, a strong grasp of percentages empowers informed decision-making and problem-solving. By understanding the different methods presented in this article and avoiding common pitfalls, you can confidently navigate the world of percentages and apply this knowledge to real-world situations. Remember to practice regularly and explore more advanced concepts to further enhance your proficiency. The more you practice, the more intuitive these calculations will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 40 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.