40 Is What Percent Of 20
News Co
Mar 20, 2025 · 5 min read
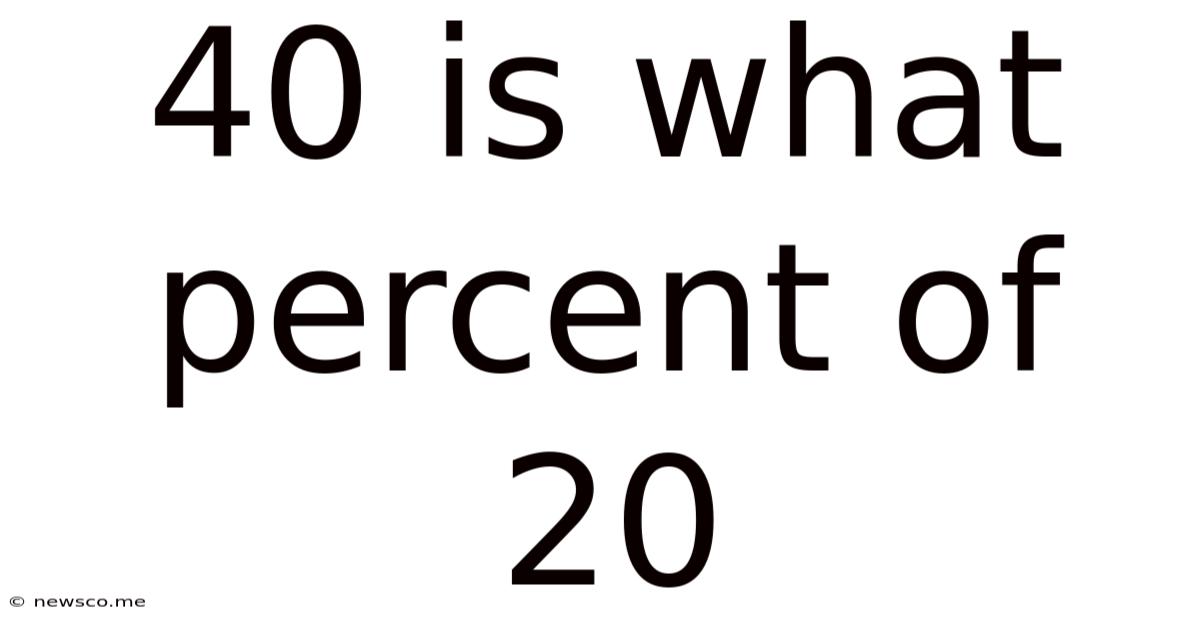
Table of Contents
40 is What Percent of 20? Understanding Percentages and Their Applications
This seemingly simple question, "40 is what percent of 20?", opens the door to a broader understanding of percentages, a fundamental concept in mathematics with widespread applications in various fields. While the immediate answer might seem counterintuitive, the process of solving it, and the underlying principles, are crucial for anyone seeking to master quantitative analysis. This article will delve deep into the solution, exploring different approaches, real-world examples, and the broader significance of percentage calculations.
Understanding Percentages: A Foundation
Before tackling the problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," literally meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding this basic principle is key to solving percentage problems. We can represent any percentage as a fraction or a decimal, and vice versa. This flexibility is what makes percentages such a versatile tool in various applications.
Solving "40 is What Percent of 20?"
The question, "40 is what percent of 20?", can be solved using several methods. Let's explore the most common and intuitive approaches:
Method 1: Using the Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 40
- Whole: 20
Plugging these values into the formula, we get:
(40 / 20) * 100 = 200%
Therefore, 40 is 200% of 20.
This result might initially seem surprising. However, it's perfectly valid. Percentages can be greater than 100%, indicating that the "part" is larger than the "whole." This often occurs when comparing values over time, showing growth or increase.
Method 2: Using Proportions
Another effective approach involves setting up a proportion:
x / 100 = 40 / 20
Where 'x' represents the unknown percentage. Solving for 'x', we cross-multiply:
20x = 4000
x = 4000 / 20
x = 200%
This method reinforces the concept of equivalent ratios and provides an alternative pathway to the solution.
Why the Result is 200%? Interpreting the Answer
The answer, 200%, signifies that 40 is twice the value of 20. This is because the "part" (40) is larger than the "whole" (20). When the percentage exceeds 100%, it indicates a value greater than the base amount.
This understanding is crucial in interpreting percentage changes and growth rates in various contexts, including:
- Financial Analysis: Tracking investment returns, evaluating profit margins, and analyzing sales growth. A 200% increase signifies a doubling of the initial investment or revenue.
- Data Analysis: Comparing data sets, visualizing trends, and identifying significant changes. A 200% increase suggests a substantial and noteworthy change.
- Scientific Research: Expressing experimental results, calculating error margins, and presenting data in a concise and understandable format.
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in our daily lives, appearing in countless contexts. Here are a few examples showcasing the practical relevance of understanding percentage calculations:
- Sales and Discounts: Retailers frequently advertise discounts as percentages (e.g., "20% off"). Understanding percentages allows consumers to calculate the actual savings.
- Taxes and Interest: Governments levy taxes on income and goods, and financial institutions charge interest on loans. These are expressed as percentages and significantly impact personal finances.
- Grade Calculations: Academic performance is often assessed using percentages, reflecting the proportion of correct answers or the overall performance relative to the total score.
- Statistical Analysis: Percentages play a critical role in statistical analysis, enabling researchers to present data in a comprehensible and meaningful manner. Examples include surveys, polls, and scientific experiments.
- Health and Fitness: Percentage body fat calculations, tracking progress in exercise programs, and assessing nutritional intake often involve percentage calculations.
- Investment and Finance: Calculating returns on investments, understanding compound interest, and analyzing financial statements heavily rely on percentage calculations. A key performance indicator (KPI) like Return on Investment (ROI) is expressed as a percentage.
- Cooking and Baking: Recipes frequently specify ingredients as percentages of the total weight or volume, offering flexibility in scaling recipes up or down.
Beyond the Basics: Advanced Percentage Calculations
While the question "40 is what percent of 20?" introduces fundamental concepts, understanding percentages extends beyond simple calculations. More complex scenarios might involve:
- Percentage Increase/Decrease: Calculating the percentage change between two values, representing growth or decline. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100. For a decrease, the formula is: [(Old Value - New Value) / Old Value] * 100.
- Compound Interest: Calculating interest earned on both the principal amount and accumulated interest over time. This concept is critical for understanding long-term investments.
- Percentage Points: Differentiating between percentage change and percentage points, particularly important when discussing changes in rates or proportions. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
Mastering these advanced concepts allows for a deeper understanding of quantitative data and its implications in various fields.
Conclusion: The Power of Percentages
The seemingly straightforward question, "40 is what percent of 20?", reveals the fundamental importance of percentages in mathematical analysis and their widespread applications across various disciplines. From everyday transactions to complex financial modeling, understanding percentages is crucial for informed decision-making and effective problem-solving. By mastering the basic principles and exploring advanced applications, one can harness the power of percentages to navigate the complexities of the quantitative world. The answer, 200%, is more than just a numerical result; it's a gateway to a deeper understanding of this essential mathematical concept. Understanding percentages is not just about solving equations, it's about interpreting data, making informed decisions, and succeeding in numerous aspects of life.
Latest Posts
Related Post
Thank you for visiting our website which covers about 40 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.