40 Of What Number Is 15
News Co
Apr 28, 2025 · 4 min read
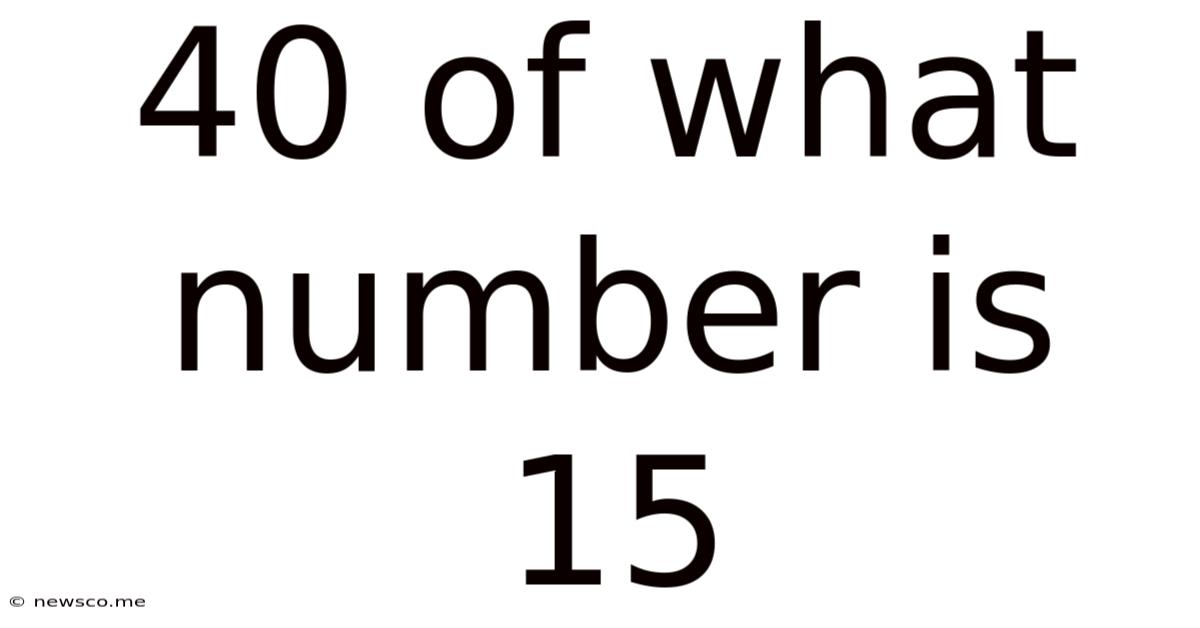
Table of Contents
40% of What Number is 15? Solving Percentage Problems
This article will delve into the solution of the problem: "40% of what number is 15?" We'll explore multiple approaches to solving this common percentage problem, clarifying the underlying concepts and providing practical examples for a comprehensive understanding. Beyond just finding the answer, we'll equip you with the skills to tackle similar percentage problems with confidence.
Understanding Percentages
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. For example, 40% can be written as 40/100 or 0.40 (as a decimal). Understanding this fundamental concept is key to solving percentage problems effectively.
Method 1: Using the Formula
The most straightforward method involves using the percentage formula:
Percentage = (Part / Whole) x 100
In our problem, we know the percentage (40%) and the part (15). We need to find the whole. Let's rearrange the formula to solve for the whole:
Whole = (Part / Percentage) x 100
Now, substitute the values:
Whole = (15 / 40) x 100
Whole = 0.375 x 100
Whole = 37.5
Therefore, 40% of 37.5 is 15.
Method 2: Using Decimals
This method converts the percentage to a decimal and then sets up an equation. Since 40% is equivalent to 0.40, we can express the problem as:
0.40 * x = 15
To solve for 'x' (the unknown number), divide both sides of the equation by 0.40:
x = 15 / 0.40
x = 37.5
Again, we find that the unknown number is 37.5.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion as follows:
40/100 = 15/x
This proportion states that the ratio of 40 to 100 is equal to the ratio of 15 to the unknown number (x). To solve for x, we can cross-multiply:
40x = 1500
Now, divide both sides by 40:
x = 1500 / 40
x = 37.5
Once more, we arrive at the solution: 37.5.
Verifying the Solution
It's always a good practice to verify the solution. Let's check if 40% of 37.5 is indeed 15:
(40/100) * 37.5 = 0.40 * 37.5 = 15
The calculation confirms our solution.
Practical Applications of Percentage Problems
Understanding how to solve percentage problems is crucial in various real-world scenarios. Here are a few examples:
-
Calculating discounts: If a store offers a 20% discount on an item originally priced at $50, you can use percentage calculations to determine the final price.
-
Determining tax amounts: Calculating sales tax or income tax involves percentage calculations.
-
Analyzing financial data: Percentage change calculations are frequently used in analyzing financial statements, such as comparing revenue growth or profit margins over time.
-
Understanding statistics: Percentages are widely used in presenting and interpreting statistical data.
-
Calculating tips and commissions: Figuring out the amount of a tip in a restaurant or a sales commission often involves percentage computations.
Beyond the Basics: More Complex Percentage Problems
While the problem "40% of what number is 15?" is relatively straightforward, percentage problems can become more complex. Let's explore a few variations:
Scenario 1: Finding the percentage increase or decrease:
Suppose a quantity increases from 20 to 25. To calculate the percentage increase:
- Find the difference: 25 - 20 = 5
- Divide the difference by the original value: 5 / 20 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
Therefore, there is a 25% increase. Similar calculations apply for percentage decrease.
Scenario 2: Multiple percentage calculations:
Imagine a scenario involving multiple discounts or taxes. For instance, a 10% discount followed by a 5% discount is not equivalent to a 15% discount. You need to apply the discounts sequentially to arrive at the correct final price.
Scenario 3: Problems involving compound interest:
Compound interest calculations require understanding exponential growth and involve more complex formulas.
Mastering Percentage Problems: Tips and Tricks
-
Practice regularly: The more you practice, the more comfortable you'll become with solving percentage problems.
-
Understand the concepts: Focus on grasping the underlying principles of percentages and ratios.
-
Use different methods: Experiment with various approaches (formula, decimals, proportions) to find the method that suits you best.
-
Check your answers: Always verify your solutions to ensure accuracy.
-
Utilize online resources: Many websites and educational platforms offer interactive exercises and tutorials on percentages.
-
Break down complex problems: If faced with a challenging problem, break it down into smaller, manageable steps.
Conclusion
Solving the problem "40% of what number is 15?" provides a foundation for understanding and tackling a wide range of percentage problems. By mastering the different methods and practicing regularly, you'll build confidence and proficiency in dealing with percentages in various contexts, from everyday calculations to more advanced mathematical applications. Remember that consistent practice and a firm grasp of the underlying concepts are key to success in mastering this essential mathematical skill. Through understanding and application, percentage problems will cease to be daunting and instead become solvable challenges. The more you engage with these problems, the more intuitive they will become, opening up a wider understanding of the numerical world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about 40 Of What Number Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.