47 5 As A Mixed Number
News Co
May 08, 2025 · 4 min read
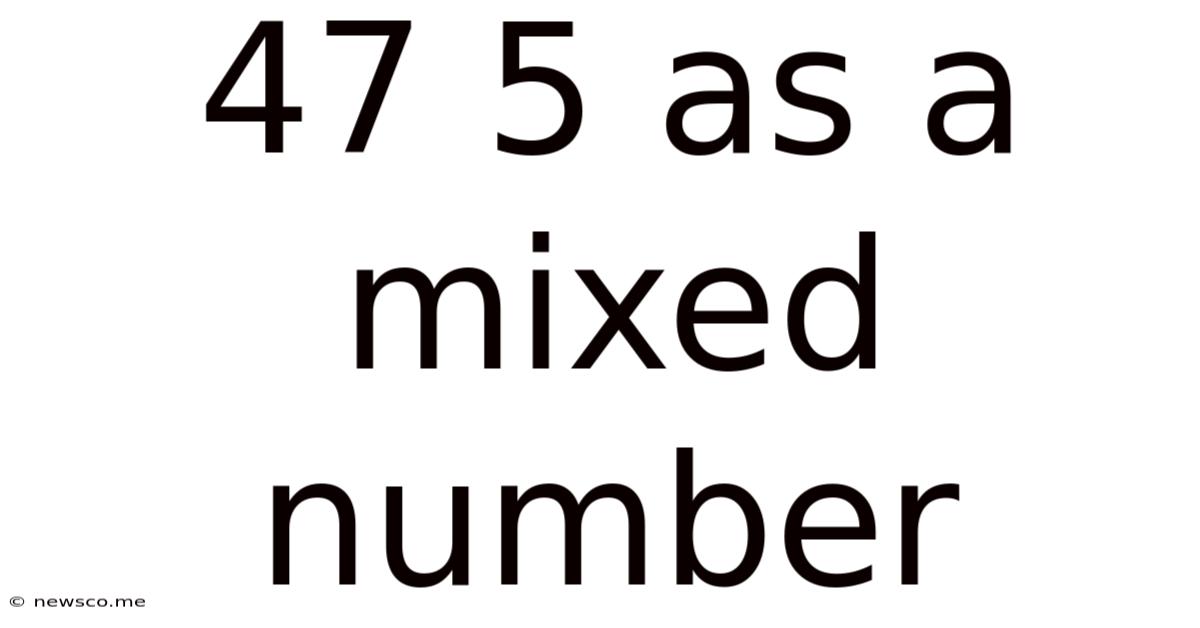
Table of Contents
47/5 as a Mixed Number: A Comprehensive Guide
Converting improper fractions to mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will delve deep into understanding and mastering the conversion of the improper fraction 47/5 into a mixed number, explaining the process step-by-step and exploring various related concepts. We'll also touch upon the importance of this skill in real-world applications and provide practical examples to solidify your understanding.
Understanding Improper Fractions and Mixed Numbers
Before we tackle the conversion of 47/5, let's clarify the definitions of improper fractions and mixed numbers.
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). In simpler terms, it represents a value greater than or equal to one. Examples include 7/4, 11/5, and, of course, 47/5.
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator is less than the denominator. Mixed numbers represent values greater than one. Examples include 1 ¾, 2 ⅔, and 3 ¼.
Converting 47/5 to a Mixed Number: The Step-by-Step Process
The conversion process involves dividing the numerator by the denominator. The quotient becomes the whole number part of the mixed number, the remainder becomes the numerator of the fractional part, and the denominator remains the same.
Step 1: Divide the Numerator by the Denominator
Divide 47 by 5:
47 ÷ 5 = 9 with a remainder of 2
Step 2: Identify the Whole Number, Numerator, and Denominator
- Whole Number: The quotient, 9, is the whole number part of our mixed number.
- Numerator: The remainder, 2, is the numerator of the fractional part.
- Denominator: The denominator remains the same as the original fraction, which is 5.
Step 3: Write the Mixed Number
Combine the whole number and the fraction to create the mixed number:
9 ²/₅
Therefore, 47/5 as a mixed number is 9 ²/₅.
Visualizing the Conversion
Imagine you have 47 identical objects, and you want to group them into sets of 5. You can create 9 complete sets of 5, leaving 2 objects remaining. This visually represents the mixed number 9 ²/₅. Each set of 5 represents the denominator, the 9 sets represent the whole number, and the remaining 2 objects represent the numerator of the fraction.
Practical Applications of Converting Improper Fractions to Mixed Numbers
The ability to convert improper fractions to mixed numbers is crucial in various real-world scenarios:
-
Measurement: When measuring lengths, volumes, or weights, you often encounter improper fractions. For instance, if a recipe calls for 11/4 cups of flour, converting it to 2 ¾ cups makes it easier to measure practically.
-
Baking and Cooking: Recipes frequently involve fractional measurements. Converting improper fractions to mixed numbers makes understanding and working with these measurements more intuitive.
-
Construction and Engineering: Precise measurements are critical in construction and engineering projects. Converting improper fractions ensures accuracy and facilitates easier calculations.
-
Everyday Life: From dividing pizzas to sharing resources, understanding fractions and mixed numbers simplifies everyday tasks.
Further Exploration of Fractions and Mixed Numbers
Let's explore some related concepts and techniques:
Converting Mixed Numbers to Improper Fractions
The reverse process – converting a mixed number to an improper fraction – is equally important. To do this:
- Multiply the whole number by the denominator.
- Add the result to the numerator.
- Keep the same denominator.
For example, converting 9 ²/₅ back to an improper fraction:
- 9 x 5 = 45
- 45 + 2 = 47
- The denominator remains 5
Therefore, 9 ²/₅ = 47/5
Simplifying Fractions
It’s always good practice to simplify fractions to their lowest terms. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. For example, 4/8 can be simplified to ½ by dividing both the numerator and denominator by their GCD, which is 4. In the case of 9 ²/₅, the fraction ²/₅ is already in its simplest form.
Adding and Subtracting Mixed Numbers
Adding and subtracting mixed numbers often involves converting them to improper fractions first to simplify the calculation. For example, to add 2 ¾ + 1 ⅔, it is often easier to convert them to improper fractions (11/4 + 5/3) before performing the addition. After finding the common denominator (12), the addition becomes (33/12 + 20/12) = 53/12 which can then be converted back into a mixed number.
Multiplying and Dividing Mixed Numbers
Similar to addition and subtraction, multiplying and dividing mixed numbers often involves converting them to improper fractions before performing the calculation.
Conclusion
Mastering the conversion of improper fractions to mixed numbers is a valuable skill with wide-ranging applications. Understanding the underlying principles, coupled with practical application, empowers you to confidently tackle various mathematical problems encountered in daily life, professional settings, and academic pursuits. Remember the key steps: divide, identify the whole number, numerator, and denominator, and then combine them to form the mixed number. Practice regularly to solidify your understanding and build fluency in this essential arithmetic skill. By utilizing this knowledge, you can navigate mathematical challenges with greater ease and efficiency, thereby enhancing your problem-solving capabilities. This skill is not only vital for academic success but also contributes significantly to practical applications in various aspects of life.
Latest Posts
Latest Posts
-
What Is The Value Of X In Each Figure
May 08, 2025
-
An Irrational Number Greater Than 10
May 08, 2025
-
What Is 20 Out Of 25 In Percentage
May 08, 2025
-
Find The Prime Factorization Of 81
May 08, 2025
-
What Is 4 Out Of 6 As A Grade
May 08, 2025
Related Post
Thank you for visiting our website which covers about 47 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.