48 Is 56 Of What Number
News Co
May 09, 2025 · 5 min read
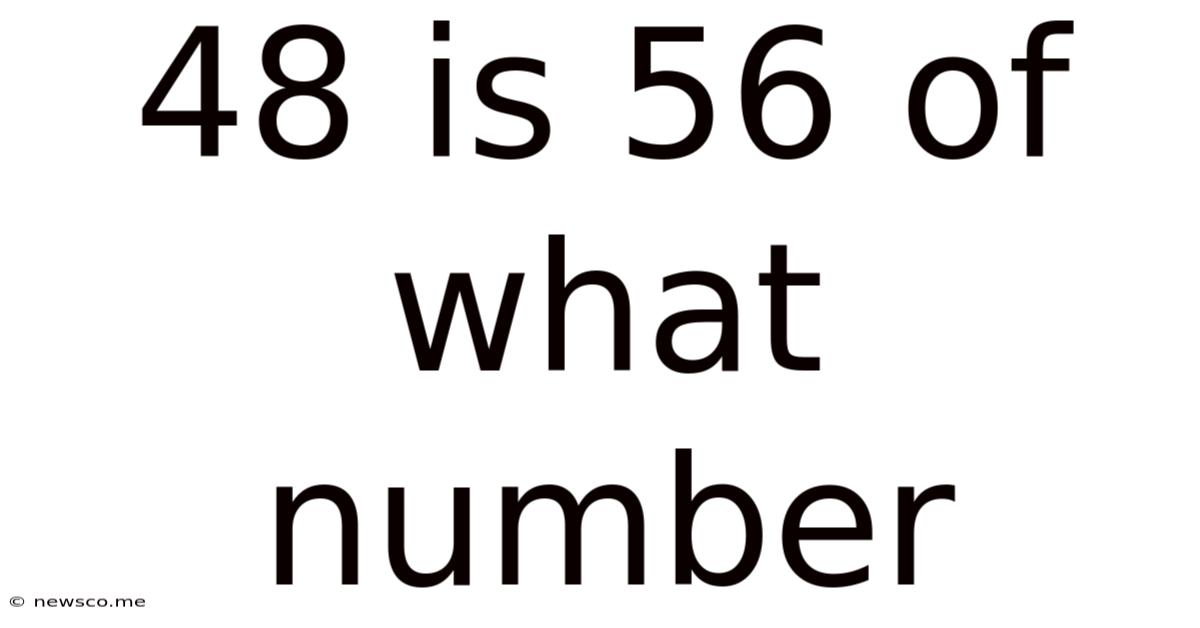
Table of Contents
48 is 56% of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill with applications across numerous fields, from finance and business to everyday life. Understanding how to calculate percentages is crucial for budgeting, calculating discounts, understanding statistics, and much more. This comprehensive guide will walk you through solving the problem "48 is 56% of what number?", explaining the underlying concepts and providing multiple methods for solving similar percentage problems. We'll explore different approaches, including using formulas, proportions, and even intuitive reasoning, ensuring you gain a thorough understanding of percentage calculations.
Understanding the Problem: Deconstructing "48 is 56% of What Number?"
Before diving into the solutions, let's break down the problem statement: "48 is 56% of what number?". This sentence translates into a mathematical equation where we need to find the unknown value. We can represent this unknown value with a variable, typically 'x'. Therefore, the problem can be rewritten as:
48 = 0.56 * x
Here, '48' represents the part, '0.56' represents the percentage (56% expressed as a decimal), and 'x' represents the whole number we are trying to find.
Method 1: Using the Percentage Formula
The most straightforward method to solve this type of problem involves using the basic percentage formula:
Part = Percentage × Whole
In our case:
- Part: 48
- Percentage: 56% or 0.56
- Whole: x (the unknown number we need to find)
Substituting these values into the formula, we get:
48 = 0.56 * x
To solve for x, we need to isolate it. We can do this by dividing both sides of the equation by 0.56:
x = 48 / 0.56
Calculating this gives us:
x ≈ 85.71
Therefore, 48 is approximately 56% of 85.71.
Understanding Decimal Conversion
It's crucial to understand the conversion from percentage to decimal. To convert a percentage to a decimal, you simply divide the percentage by 100. For example:
- 56% = 56/100 = 0.56
- 25% = 25/100 = 0.25
- 10% = 10/100 = 0.10
This conversion is necessary to use the percentage formula effectively.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion using the given information:
48/x = 56/100
This proportion reads as "48 is to x as 56 is to 100". To solve for x, we can cross-multiply:
48 * 100 = 56 * x
4800 = 56x
Now, divide both sides by 56:
x = 4800 / 56
x ≈ 85.71
Again, we find that 48 is approximately 56% of 85.71.
Advantages of the Proportion Method
The proportion method can be particularly helpful for visualizing the relationship between the parts and the whole. It clearly demonstrates the equivalence between the two ratios.
Method 3: Working Backwards from the Percentage
We can also approach this problem by considering the meaning of percentage. 56% means 56 out of 100. If 56 out of 100 represents the equivalent of 48, we can set up a ratio:
56/100 = 48/x
This is essentially the same proportion we used in Method 2, leading to the same solution: x ≈ 85.71
Intuitive Understanding
This method helps build an intuitive understanding of percentages. It allows you to directly relate the percentage to its fractional equivalent and then solve for the unknown.
Method 4: Using a Calculator
Most calculators have a percentage function that simplifies these calculations. You can input the problem directly using the percentage function, typically represented by a '%' symbol. The specific steps will vary depending on the calculator model, but the general approach is to input 48, then the division symbol, then 56, and finally press the '%' button. The calculator will automatically perform the necessary division and provide the answer.
Calculator Efficiency
While this is the quickest method, it's essential to understand the underlying mathematical principles to solve percentage problems without a calculator and to comprehend the results.
Addressing Potential Errors and Challenges
When working with percentages, certain common errors can arise. Here are some important points to keep in mind:
-
Decimal Conversion: Always ensure you correctly convert percentages to decimals before performing calculations. A simple mistake in this step can lead to significantly inaccurate results.
-
Order of Operations: Pay close attention to the order of operations (PEMDAS/BODMAS) when solving more complex percentage problems.
-
Rounding: Be mindful of rounding errors. When rounding to a specific number of decimal places, it's crucial to understand the implications for accuracy.
-
Interpreting Results: Always interpret your results within the context of the problem. A calculated value of 85.71 in this context represents the whole number of which 48 is 56%.
Expanding the Application of Percentage Calculations
The techniques discussed above aren't limited to this specific problem. They are applicable to a wide array of percentage calculations, including:
- Calculating discounts: Determining the sale price of an item after a percentage discount.
- Calculating tax: Figuring out the total cost of an item after adding sales tax.
- Calculating tips: Determining the appropriate tip amount in a restaurant.
- Analyzing financial statements: Understanding financial ratios and percentages in business contexts.
- Interpreting statistical data: Analyzing survey results and other statistical data represented as percentages.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is crucial for success in many aspects of life. Understanding the underlying concepts and utilizing various methods, including formulas, proportions, and intuitive reasoning, will enable you to tackle percentage problems with confidence. Remember to always check your work, pay attention to detail, and understand the implications of rounding. By consistently applying these techniques, you will develop a strong foundation in percentage calculations, paving the way for more advanced mathematical problem-solving. This guide provides a thorough foundation, encouraging you to practice and refine your skills to become proficient in this essential mathematical concept. The ability to confidently and accurately solve percentage problems will undoubtedly enhance your understanding of numerical relationships and broaden your problem-solving capabilities.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 48 Is 56 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.