4a 6b 10 2a 4b 12 What Does 12a Equal
News Co
Mar 26, 2025 · 5 min read
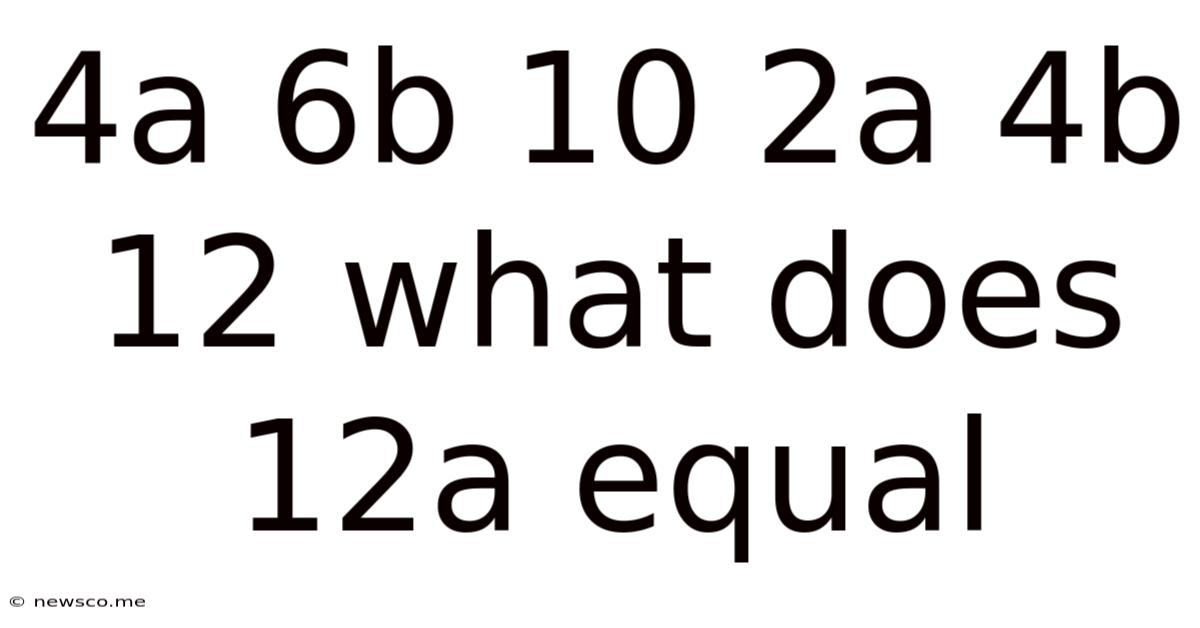
Table of Contents
Decoding the Mathematical Puzzle: 4a 6b 10, 2a 4b 12 - What Does 12a Equal?
This article delves into the intriguing mathematical puzzle presented by the equations "4a + 6b = 10" and "2a + 4b = 12." Our primary goal is to determine the value of "12a." This isn't simply a matter of plugging numbers into a formula; it requires a strategic approach involving solving a system of linear equations. We'll explore different methods for achieving this solution and discuss the underlying mathematical principles involved. This problem provides a fantastic opportunity to reinforce fundamental algebraic concepts and problem-solving skills.
Understanding Systems of Linear Equations
Before we tackle the specific problem, let's lay the groundwork. The core of this puzzle lies in solving a system of linear equations. A system of linear equations is a set of two or more linear equations with the same variables. In our case, the variables are 'a' and 'b'. The equations are:
- Equation 1: 4a + 6b = 10
- Equation 2: 2a + 4b = 12
Our objective is to find the values of 'a' and 'b' that simultaneously satisfy both equations. Once we have these values, calculating '12a' becomes straightforward.
Method 1: Elimination Method
The elimination method, also known as the addition method, is a powerful technique for solving systems of linear equations. The goal is to eliminate one variable by manipulating the equations so that when they're added or subtracted, one variable cancels out.
Let's apply this to our problem:
-
Simplify Equation 2: Notice that Equation 2 can be simplified by dividing both sides by 2: a + 2b = 6
-
Eliminate 'a': To eliminate 'a', we can multiply the simplified Equation 2 by -4: -4a - 8b = -24
-
Add the Equations: Now, add this modified Equation 2 to Equation 1: (4a + 6b) + (-4a - 8b) = 10 + (-24) This simplifies to: -2b = -14
-
Solve for 'b': Divide both sides by -2: b = 7
-
Substitute 'b' back into an equation: Now that we have the value of 'b', substitute it back into either Equation 1 or the simplified Equation 2 to solve for 'a'. Let's use the simplified Equation 2: a + 2(7) = 6 a + 14 = 6 a = 6 - 14 a = -8
-
Calculate 12a: Finally, we can calculate 12a: 12a = 12 * (-8) = -96
Therefore, using the elimination method, we find that 12a = -96.
Method 2: Substitution Method
The substitution method involves solving one equation for one variable and then substituting that expression into the other equation.
-
Solve for 'a' in Equation 2: Let's solve the simplified Equation 2 (a + 2b = 6) for 'a': a = 6 - 2b
-
Substitute into Equation 1: Substitute this expression for 'a' into Equation 1: 4(6 - 2b) + 6b = 10
-
Solve for 'b': Expand and simplify the equation: 24 - 8b + 6b = 10 24 - 2b = 10 -2b = -14 b = 7
-
Substitute 'b' to find 'a': Substitute the value of 'b' (7) back into the expression for 'a': a = 6 - 2(7) a = 6 - 14 a = -8
-
Calculate 12a: As before, 12a = 12 * (-8) = -96
Again, we arrive at the same conclusion: 12a = -96.
Method 3: Graphical Method
While less practical for complex systems, the graphical method provides a visual representation of the solution. Each equation represents a straight line on a graph. The point where the lines intersect represents the solution (the values of 'a' and 'b' that satisfy both equations).
To use this method, you would need to rearrange both equations into the slope-intercept form (y = mx + b), where 'a' would be the x-coordinate and 'b' would be the y-coordinate. Plot both lines on a graph. The point of intersection would give you the values of 'a' and 'b', allowing you to calculate 12a. This method is less precise than the algebraic methods, especially if the solution involves non-integer values.
Verifying the Solution
It's always good practice to verify your solution by substituting the values of 'a' and 'b' back into the original equations:
- Equation 1: 4(-8) + 6(7) = -32 + 42 = 10 (Correct)
- Equation 2: 2(-8) + 4(7) = -16 + 28 = 12 (Correct)
Both equations are satisfied, confirming that a = -8 and b = 7 is the correct solution.
Expanding on the Concepts: Applications of Linear Equations
The ability to solve systems of linear equations is crucial in various fields:
- Engineering: Designing structures, analyzing circuits, and modeling dynamic systems.
- Economics: Analyzing market equilibrium, forecasting economic trends, and optimizing resource allocation.
- Computer Science: Developing algorithms, creating simulations, and implementing machine learning models.
- Physics: Solving problems in mechanics, electricity, and thermodynamics.
- Chemistry: Determining the composition of mixtures and balancing chemical reactions.
Understanding and mastering techniques like elimination and substitution are fundamental building blocks for more advanced mathematical concepts and applications.
Conclusion: The Power of Problem Solving
The seemingly simple puzzle, "4a + 6b = 10, 2a + 4b = 12, what does 12a equal?", highlights the power of systematic problem-solving and the importance of understanding fundamental mathematical principles. We've explored three different methods to arrive at the solution (12a = -96), demonstrating the versatility of algebraic techniques. Beyond the specific answer, this problem serves as a valuable exercise in strengthening your algebraic skills and appreciating the wide-ranging applications of linear equations in various disciplines. Remember to always check your work and explore different approaches to solidify your understanding. This analytical approach will serve you well in tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4a 6b 10 2a 4b 12 What Does 12a Equal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.