5 15 6 18 7 21 8
News Co
Apr 10, 2025 · 5 min read
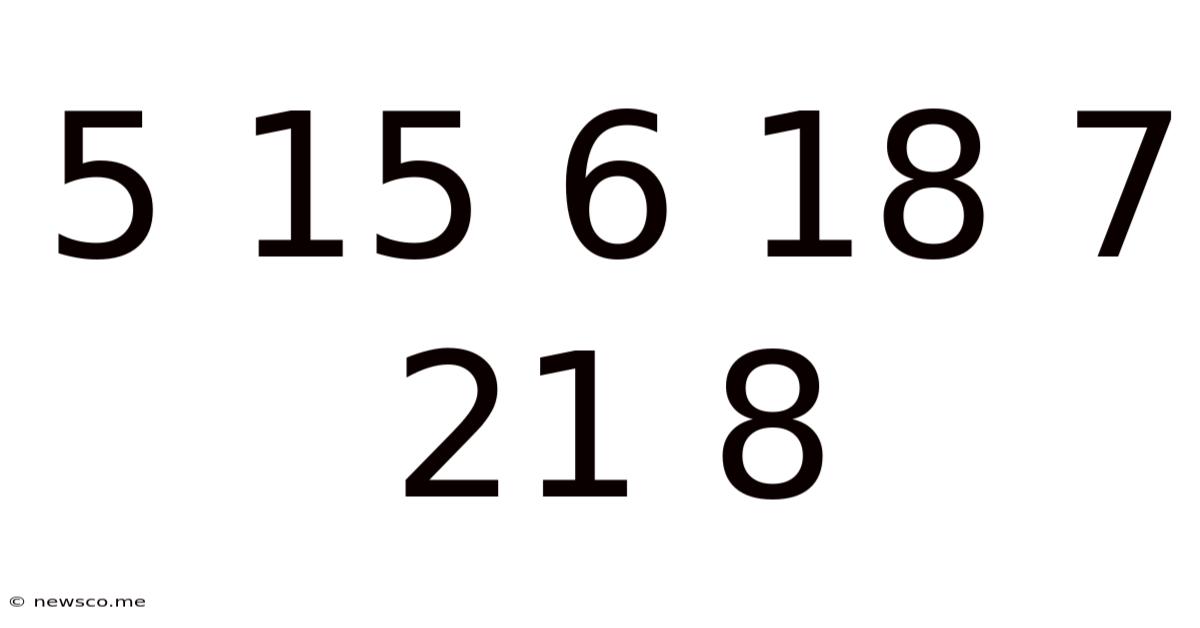
Table of Contents
Unlocking the Pattern: A Deep Dive into the Sequence 5 15 6 18 7 21 8
The seemingly simple sequence 5, 15, 6, 18, 7, 21, 8… presents a fascinating puzzle. At first glance, it might appear random. However, a closer examination reveals an underlying pattern, a mathematical rhythm hidden within the seemingly chaotic arrangement of numbers. This article will delve into the intricacies of this sequence, exploring its structure, uncovering the logic behind its construction, and ultimately demonstrating how to predict future terms. We’ll also touch on the broader mathematical concepts it embodies and how similar patterns can be found in diverse fields.
Deciphering the Dual Pattern: Addition and Multiplication
The key to understanding this sequence lies in recognizing that it's not a single, continuous progression but rather a cleverly interwoven combination of two distinct patterns operating concurrently. Let’s break down the sequence into two interwoven subsequences:
Subsequence 1: 5, 6, 7, 8…
This subsequence is simply an arithmetic progression where each term is increased by 1. It's a straightforward linear sequence, easily predictable. The next term would be 9, followed by 10, and so on.
Subsequence 2: 15, 18, 21…
This subsequence also displays a clear pattern. Each term is increased by 3. This is also an arithmetic progression, but with a different common difference than the first subsequence. The next term in this sequence would be 24, followed by 27, and so on.
The Interleaved Structure: A Symphony of Sequences
Now, the brilliance of the original sequence 5, 15, 6, 18, 7, 21, 8… becomes apparent. It's an interleaving of these two arithmetic progressions. The sequence alternates between the terms of Subsequence 1 and Subsequence 2.
- Term 1: 5 (from Subsequence 1)
- Term 2: 15 (from Subsequence 2)
- Term 3: 6 (from Subsequence 1)
- Term 4: 18 (from Subsequence 2)
- Term 5: 7 (from Subsequence 1)
- Term 6: 21 (from Subsequence 2)
- Term 7: 8 (from Subsequence 1)
This interleaving creates the illusion of complexity, masking the underlying simplicity of the two constituent sequences.
Predicting Future Terms: Extending the Pattern
Armed with this understanding, we can now confidently predict future terms in the sequence. We simply continue both subsequences and interleave them:
- Term 8: 24 (from Subsequence 2)
- Term 9: 9 (from Subsequence 1)
- Term 10: 27 (from Subsequence 2)
- Term 11: 10 (from Subsequence 1)
- Term 12: 30 (from Subsequence 2)
- Term 13: 11 (from Subsequence 1)
- Term 14: 33 (from Subsequence 2)
- and so on...
The sequence extends infinitely, following the established pattern of alternating between the two arithmetic progressions.
Beyond the Obvious: Exploring Deeper Mathematical Concepts
While the primary pattern is straightforward, the sequence touches upon several important mathematical concepts:
-
Arithmetic Progressions: The foundation of the sequence lies in the understanding and application of arithmetic progressions. These sequences are fundamental to many areas of mathematics, including algebra, calculus, and number theory.
-
Sequences and Series: The sequence provides a concrete example of how different sequences can be combined to create more complex patterns. This concept is crucial in understanding infinite series and their convergence or divergence.
-
Pattern Recognition: The ability to identify patterns is a vital skill in mathematics and problem-solving. This sequence serves as a great exercise in honing this skill. The initial seeming randomness requires careful observation and analysis to reveal the underlying structure.
-
Recursive Definitions: While we've described the sequence iteratively, it could also be defined recursively. A recursive definition would explicitly define the relationship between successive terms. For example, a recursive definition for the whole sequence would require specifying rules for both odd and even numbered terms, referencing the preceding terms.
Applications in Real-World Scenarios
While this specific sequence may not have a direct application in a specific scientific or engineering field, the underlying principles are widely applicable. The concept of interleaving sequences and recognizing patterns within seemingly random data appears in various domains:
-
Data Analysis: Identifying patterns in data sets is crucial in fields like finance, meteorology, and medicine. The ability to dissect complex data into simpler, underlying patterns, similar to how we approached this sequence, is a core competency for data analysts.
-
Signal Processing: Signals, both auditory and visual, can often be decomposed into simpler constituent signals. Understanding how to separate and analyze these underlying components is fundamental to signal processing.
-
Cryptography: Certain cryptographic techniques rely on the manipulation and encoding of sequences. The concepts of pattern recognition and sequence analysis are therefore relevant to this field.
-
Computer Science: Algorithms often rely on iterating through sequences and identifying patterns. Understanding and manipulating sequences is essential to programming and algorithm design.
Expanding the Horizons: Creating Your Own Sequences
The exploration of this sequence provides a foundation for creating your own complex yet elegant patterns. By combining different arithmetic progressions or other types of sequences (geometric, Fibonacci, etc.) and interleaving them strategically, you can generate an infinite variety of unique sequences. Experiment with different common differences and starting values to see the range of patterns that can be created. This exercise strengthens both mathematical understanding and creative problem-solving skills.
Conclusion: The Beauty of Hidden Order
The sequence 5, 15, 6, 18, 7, 21, 8… initially seems like a collection of random numbers. However, through careful analysis, we uncovered a hidden beauty—the elegant interplay of two simple arithmetic progressions. This reveals the power of pattern recognition and the importance of understanding underlying mathematical structures. The sequence serves as a captivating example of how seemingly complex phenomena can be reduced to fundamental principles, highlighting the mathematical elegance that often underpins the apparent randomness of the world around us. This understanding extends beyond simple number sequences and has broad implications in various fields, from data analysis to computer science. The journey of deciphering this sequence demonstrates the beauty of hidden order and the rewarding experience of unraveling mathematical puzzles. The principles learned here can be applied to countless other mathematical problems and provide a valuable foundation for further exploration in the fascinating world of sequences and patterns.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 15 6 18 7 21 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.