5/8 As A Percent And Decimal
News Co
Mar 28, 2025 · 6 min read
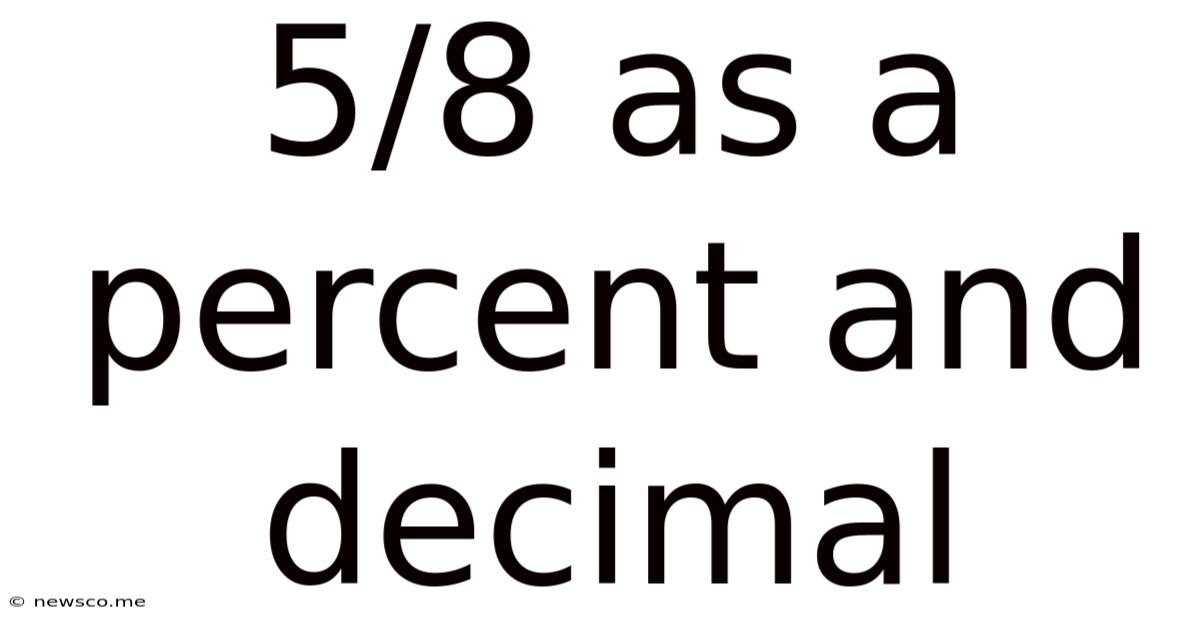
Table of Contents
5/8 as a Percent and Decimal: A Comprehensive Guide
Understanding fractions, decimals, and percentages is fundamental to various aspects of life, from everyday calculations to complex financial analyses. This comprehensive guide delves into the conversion of the fraction 5/8 into its decimal and percentage equivalents, exploring the underlying methods and providing practical applications. We'll also examine related concepts and offer tips to master these conversions.
Understanding Fractions, Decimals, and Percentages
Before diving into the specific conversion of 5/8, let's solidify our understanding of these three interconnected representations of numbers.
Fractions
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 5/8, 5 is the numerator and 8 is the denominator. This means we have 5 parts out of a total of 8 equal parts.
Decimals
Decimals represent numbers using a base-ten system. The decimal point separates the whole number part from the fractional part. Each position to the right of the decimal point represents a decreasing power of 10 (tenths, hundredths, thousandths, etc.). For example, 0.625 represents six tenths, two hundredths, and five thousandths.
Percentages
A percentage is a fraction expressed as a portion of 100. It's denoted by the symbol "%". Percentages are commonly used to represent proportions, rates, or changes. For instance, 62.5% means 62.5 out of 100.
Converting 5/8 to a Decimal
There are two primary methods to convert the fraction 5/8 to its decimal equivalent:
Method 1: Long Division
This method involves dividing the numerator (5) by the denominator (8).
-
Set up the long division: Place the numerator (5) inside the division symbol and the denominator (8) outside. Since 5 is smaller than 8, we add a decimal point to 5 and add a zero to make it 5.0.
-
Perform the division: 8 goes into 50 six times (6 x 8 = 48). Subtract 48 from 50, leaving a remainder of 2.
-
Add another zero: Bring down another zero to make the remainder 20.
-
Continue the division: 8 goes into 20 two times (2 x 8 = 16). Subtract 16 from 20, leaving a remainder of 4.
-
Add another zero: Bring down another zero to make the remainder 40.
-
Final division: 8 goes into 40 five times (5 x 8 = 40). The remainder is 0, indicating the division is complete.
Therefore, 5/8 = 0.625.
Method 2: Equivalent Fractions
This method involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). While not always straightforward, it can be useful for certain fractions. Unfortunately, 8 does not easily convert to a power of 10. Therefore, long division is the more practical method in this case.
Converting 5/8 to a Percentage
Once we have the decimal equivalent (0.625), converting to a percentage is straightforward. We simply multiply the decimal by 100 and add the "%" symbol.
0.625 x 100 = 62.5%
Therefore, 5/8 is equivalent to 62.5%.
Practical Applications of 5/8, 0.625, and 62.5%
Understanding these equivalent representations is crucial in various real-world scenarios:
-
Measurements: If you're working with measurements, knowing that 5/8 of an inch is equal to 0.625 inches or 62.5% of an inch can be extremely helpful for precision.
-
Discounts: A 62.5% discount on an item means you'll pay only 37.5% of the original price. Understanding the decimal equivalent (0.375) allows for easy calculation.
-
Financial Calculations: Interest rates, loan payments, and investment returns are frequently expressed as percentages. Converting them to decimals allows for accurate calculations.
-
Data Analysis: Representing data as percentages allows for easy comparison and interpretation of proportions.
-
Probability: Probabilities are often represented as fractions or decimals, and converting them to percentages can aid in understanding the likelihood of an event occurring.
Mastering Fraction, Decimal, and Percentage Conversions
To become proficient in these conversions, consistent practice is key. Here are some tips:
-
Memorize common fractions and their decimal/percentage equivalents: Learning the equivalents for fractions like 1/2, 1/4, 1/8, 3/4, etc., will significantly speed up your calculations.
-
Practice regularly: Work through various conversion problems, starting with simple fractions and gradually increasing the complexity.
-
Use online tools and calculators: While it's important to understand the underlying methods, online tools can help verify your answers and provide additional practice. However, always focus on learning the process, rather than just relying on the tools.
-
Understand the relationship between fractions, decimals, and percentages: The key to mastering these conversions lies in grasping their interconnectedness. Each representation provides a different perspective on the same numerical value.
Advanced Concepts and Related Topics
This section explores more advanced concepts related to fractions, decimals, and percentages:
Working with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 2 5/8). To convert a mixed number to a decimal or percentage, first convert the mixed number to an improper fraction (in this case, 21/8). Then, use the methods described earlier to convert to a decimal and percentage.
Converting Repeating Decimals
Some fractions result in repeating decimals (e.g., 1/3 = 0.333...). Understanding how to represent these repeating decimals and convert them back to fractions is an important skill.
Percentage Increase and Decrease
Calculating percentage increase or decrease involves determining the change in a value relative to its original value. This requires understanding how to work with percentages and decimals in a practical context.
Compound Interest
Understanding compound interest requires a solid grasp of percentage calculations, as interest is calculated repeatedly on the principal plus accumulated interest.
Applications in Various Fields
The concepts discussed here have far-reaching applications across numerous fields, including:
-
Engineering: Precise calculations are essential in engineering, requiring a strong understanding of fractions, decimals, and percentages.
-
Finance: Financial modeling, investment analysis, and risk management rely heavily on accurate numerical calculations.
-
Science: Data analysis and experimental results often require conversions between these numerical representations.
-
Cooking and Baking: Accurate measurements are crucial in cooking and baking, often requiring the use of fractions and their decimal equivalents.
Conclusion
Converting 5/8 to its decimal (0.625) and percentage (62.5%) equivalent is a fundamental skill with widespread applications. By understanding the methods involved and practicing regularly, you can master these conversions and apply them effectively in various contexts. Remember to focus on the underlying principles to build a strong foundation and solve a wide array of numerical problems. The more you practice, the more confident and efficient you'll become in handling these essential mathematical concepts. Mastering these skills will undoubtedly enhance your problem-solving abilities and improve your overall mathematical literacy.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 5/8 As A Percent And Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.