5 8 Divided By 2 In Fraction
News Co
May 08, 2025 · 4 min read
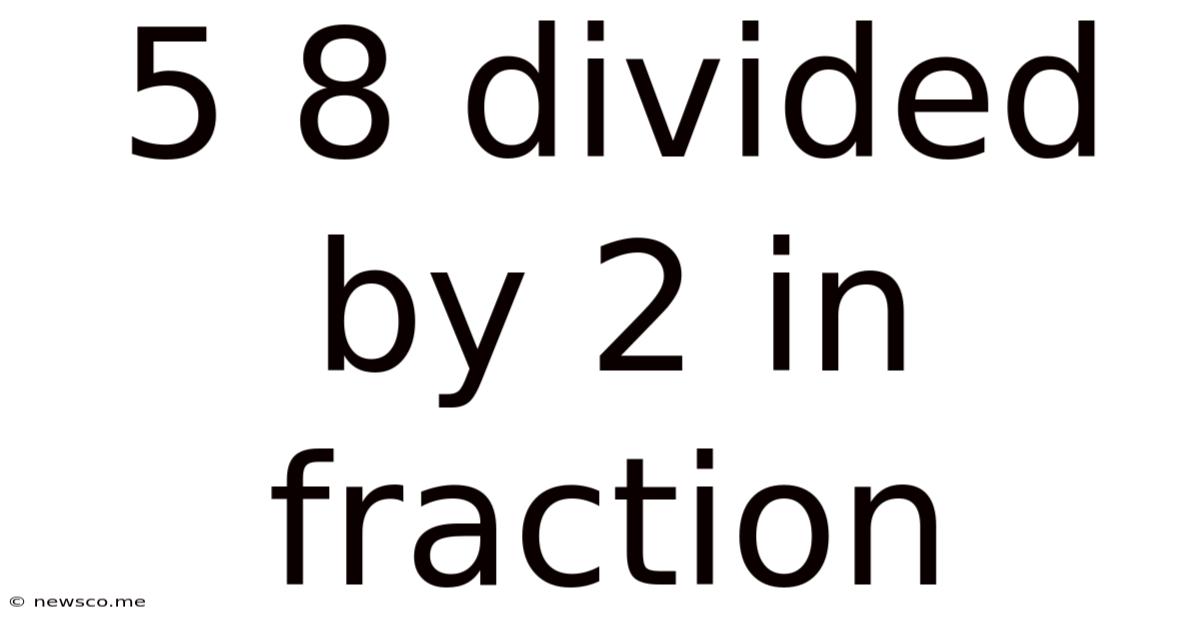
Table of Contents
5 8/2: Demystifying Mixed Number Division
Dividing mixed numbers can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through solving 5 8/2, explaining the steps involved, and exploring the underlying mathematical principles. We'll also delve into various methods for tackling similar problems, ensuring you develop a strong grasp of this fundamental arithmetic operation.
Understanding Mixed Numbers
Before diving into the division, let's solidify our understanding of mixed numbers. A mixed number combines a whole number and a fraction. In our case, 5 8/2 represents five whole units and eight halves. This can be visualized as five complete objects and eight half-objects. The key to efficiently dividing mixed numbers is converting them into improper fractions.
Converting Mixed Numbers to Improper Fractions
An improper fraction has a numerator larger than or equal to its denominator. To convert a mixed number to an improper fraction, follow these steps:
-
Multiply the whole number by the denominator: In 5 8/2, we multiply 5 (the whole number) by 2 (the denominator). This gives us 10.
-
Add the numerator: Add the result from step 1 to the numerator of the fraction (8). 10 + 8 = 18.
-
Keep the same denominator: The denominator remains unchanged. Therefore, 5 8/2 converts to the improper fraction 18/2.
Dividing by a Whole Number: The Simple Case
Now that we've transformed our mixed number into an improper fraction, the division becomes much simpler. We are essentially dividing 18/2 by 1 (since 2 is equivalent to 2/1). The calculation is straightforward:
18/2 ÷ 1 = 18/2 = 9
Therefore, 5 8/2 divided by 1 is equal to 9. Notice that this division is equivalent to simply evaluating the improper fraction, 18/2, and finding its simplified value.
The General Case: Dividing Mixed Numbers by Mixed Numbers
Let's extend our understanding to a more general scenario, dividing a mixed number by another mixed number. For instance, imagine we have to solve 5 8/2 ÷ 2 1/2. This problem requires a slightly more involved process.
Step 1: Convert to Improper Fractions
- 5 8/2 converts to 18/2 as shown previously.
- 2 1/2 converts to (2 * 2 + 1)/2 = 5/2.
Step 2: Invert and Multiply
Dividing by a fraction is equivalent to multiplying by its reciprocal (the fraction flipped upside down). So we change the division problem to a multiplication problem:
18/2 ÷ 5/2 = 18/2 * 2/5
Step 3: Simplify and Multiply
Before multiplying, look for opportunities to simplify. In this case, we can cancel the common factor of '2' from both the numerator and denominator:
(18/2) * (2/5) = (18/1) * (1/5) = 18/5
Step 4: Convert Back to a Mixed Number (Optional)
The answer, 18/5, is an improper fraction. To express it as a mixed number, we perform division:
18 ÷ 5 = 3 with a remainder of 3.
Therefore, 18/5 is equivalent to the mixed number 3 3/5. This means 5 8/2 ÷ 2 1/2 = 3 3/5.
Practical Applications and Real-World Examples
Understanding mixed number division is crucial in various practical applications. Consider the following examples:
- Recipe Scaling: If a recipe calls for 2 1/2 cups of flour and you want to make only half the recipe, you need to divide 2 1/2 by 2.
- Measuring Materials: Construction projects often require precise measurements. Dividing lengths expressed as mixed numbers is a common task.
- Data Analysis: Calculating averages involving mixed number data (e.g., average time spent on a task) demands proficiency in mixed number division.
- Geometry and Area Calculations: Finding areas of irregular shapes might involve computations using mixed numbers.
Advanced Concepts and Further Exploration
While we've focused on the basic principles, understanding mixed number division opens the door to more advanced concepts:
- Complex Fractions: These involve fractions within fractions, often requiring multiple steps of conversion and simplification.
- Algebraic Expressions: Mixed numbers can appear within algebraic equations, requiring similar conversion and manipulation techniques.
- Division with Multiple Mixed Numbers: Problems involving dividing by multiple mixed numbers require a methodical approach, applying the same principles sequentially.
Troubleshooting Common Mistakes
Common errors in mixed number division include:
- Incorrect Conversion to Improper Fractions: Carefully follow the steps for conversion to avoid errors.
- Forgetting to Invert and Multiply: Remember that dividing by a fraction is equivalent to multiplying by its reciprocal.
- Simplification Errors: Always look for opportunities to simplify before multiplying to minimize calculations and potential errors.
Conclusion: Mastering Mixed Number Division
Mastering mixed number division empowers you to tackle complex problems confidently. By understanding the steps involved – converting to improper fractions, inverting and multiplying, and simplifying – you can successfully solve a wide range of problems. Regular practice and applying these concepts to real-world situations will solidify your understanding and improve your proficiency in this essential mathematical skill. Remember to always double-check your work and look for opportunities to simplify throughout the calculation. This detailed guide provides a comprehensive foundation for confidently handling mixed number divisions in various contexts.
Latest Posts
Latest Posts
-
5 Futov 4 Dyuyma V Sm
May 09, 2025
-
Are Same Side Exterior Angles Congruent
May 09, 2025
-
How To Find The Apothem Of A Triangle
May 09, 2025
-
What Is The Greatest Common Factor Of 32
May 09, 2025
-
Place Value Value Of The Underlined Digit
May 09, 2025
Related Post
Thank you for visiting our website which covers about 5 8 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.