5 And 3/5 As A Decimal
News Co
Apr 17, 2025 · 5 min read
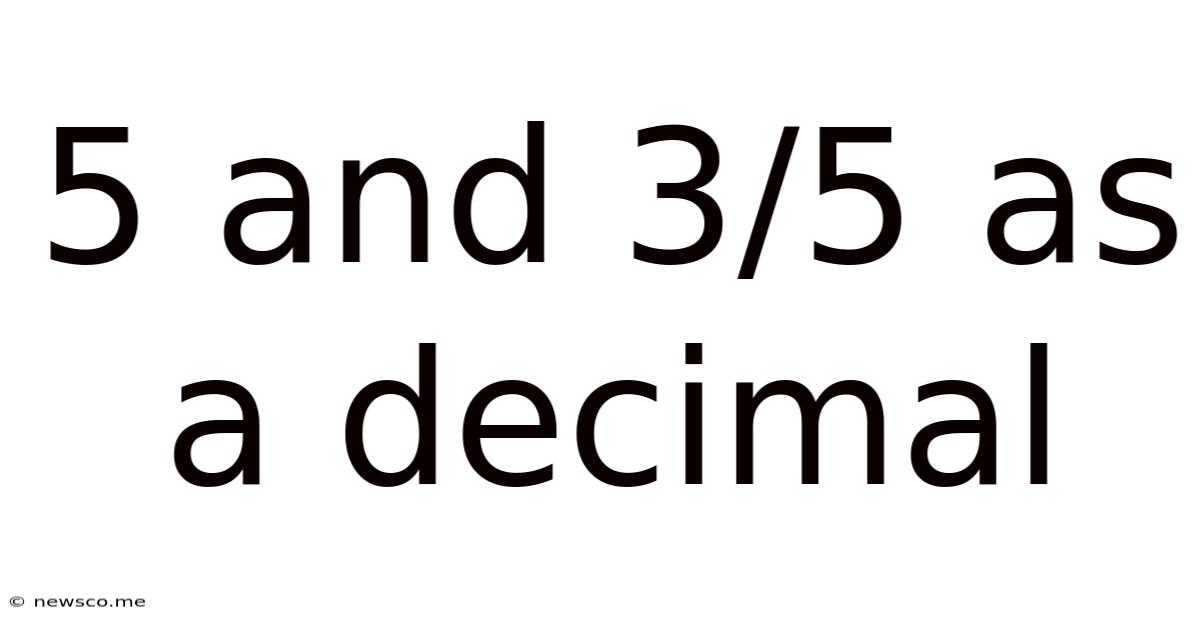
Table of Contents
5 and 3/5 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics and numerous real-world applications. This comprehensive guide delves into the conversion of the mixed number 5 and 3/5 into its decimal form, exploring the process step-by-step and providing context for broader understanding. We'll also explore various methods, discuss the importance of decimal representation, and touch upon practical applications.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's establish a clear understanding of the terms involved.
Mixed Number: A mixed number combines a whole number and a fraction, such as 5 and 3/5. It represents a quantity greater than one.
Decimal: A decimal number uses a base-ten system, employing a decimal point to separate the whole number part from the fractional part. For instance, 5.6 is a decimal number where 5 is the whole number and 6 is the tenth part.
The core of this process involves understanding that fractions represent parts of a whole. The denominator (the bottom number in a fraction) indicates the number of equal parts the whole is divided into, while the numerator (the top number) indicates how many of those parts are being considered.
Converting 5 and 3/5 to a Decimal: Step-by-Step
There are two primary methods for converting 5 and 3/5 to its decimal equivalent:
Method 1: Converting the Fraction to a Decimal and Adding the Whole Number
This is perhaps the most straightforward approach. We first convert the fraction 3/5 to its decimal form, and then add the whole number 5.
-
Divide the numerator by the denominator: Divide 3 (the numerator) by 5 (the denominator): 3 ÷ 5 = 0.6
-
Add the whole number: Add the result (0.6) to the whole number part (5): 5 + 0.6 = 5.6
Therefore, 5 and 3/5 as a decimal is 5.6.
Method 2: Converting the Mixed Number to an Improper Fraction and then to a Decimal
This method involves converting the mixed number into an improper fraction first and then performing the division.
-
Convert to an improper fraction: To convert 5 and 3/5 to an improper fraction, we multiply the whole number (5) by the denominator (5) and add the numerator (3). This result becomes the new numerator, while the denominator remains the same.
(5 x 5) + 3 = 28
The improper fraction is 28/5.
-
Divide the numerator by the denominator: Divide 28 (the numerator) by 5 (the denominator): 28 ÷ 5 = 5.6
Again, we arrive at the same answer: 5 and 3/5 as a decimal is 5.6.
Why is Decimal Representation Important?
Decimal representation offers several advantages over fractional representation, particularly in various applications:
-
Ease of Comparison: Comparing decimal numbers is often easier than comparing fractions. For example, it’s immediately clear that 5.6 is larger than 5.5. Comparing 5 and 3/5 to 5 and 1/2 might require a bit more mental calculation.
-
Calculations: Decimal numbers are generally easier to use in calculations, particularly when using calculators or computers. Adding, subtracting, multiplying, and dividing decimals are straightforward operations.
-
Real-world Applications: Many real-world measurements and values are expressed in decimals. Consider money (dollars and cents), weights, and measures. Decimal representation provides a consistent and easily understandable format for these measurements.
-
Data Analysis and Presentation: In data analysis and presentation, decimals are frequently used for clarity and consistency. It simplifies comparisons and trends in datasets.
Practical Applications of Decimal Representation: Real-world Examples
Decimal numbers are ubiquitous in our daily lives. Here are some examples showcasing their practical applications:
-
Finance: Money is universally represented in decimal form. For example, $5.60 represents five dollars and sixty cents.
-
Measurements: Lengths, weights, and volumes are often expressed in decimals. A piece of wood measuring 5.6 meters is easily understood.
-
Science: Scientific measurements and calculations frequently use decimals to express precise quantities.
-
Engineering: Engineering designs and calculations heavily rely on decimal representation for precision and accuracy.
-
Technology: Computer programming and data representation utilize decimals extensively.
-
Sports: In many sports, statistics such as batting averages or scoring averages are expressed as decimals (e.g., a batting average of .280).
Further Exploration of Fraction to Decimal Conversions
While we've focused on 5 and 3/5, the principles discussed apply broadly to converting any mixed number or fraction to a decimal. The key is understanding the relationship between the numerator and the denominator, and the process of division. For fractions with denominators that are not easily divisible (e.g., 7, 11), the resulting decimal may be a repeating or non-terminating decimal.
Beyond the Basics: Advanced Decimal Concepts
To further expand your understanding, consider exploring the following advanced concepts:
-
Repeating Decimals: Understanding how to represent fractions like 1/3 (0.333...) as decimals.
-
Non-terminating Decimals: Learning about irrational numbers and their infinite non-repeating decimal representations.
-
Significant Figures: Mastering the concept of significant figures for precision and accuracy in measurements and calculations.
-
Scientific Notation: Learning how to express very large or very small numbers using scientific notation.
By understanding these concepts, you’ll enhance your mathematical abilities and be better equipped to handle various numerical tasks efficiently.
Conclusion
Converting 5 and 3/5 to its decimal equivalent (5.6) is a straightforward process using division. This seemingly simple conversion underscores the fundamental connection between fractions and decimals – two essential numerical representations with diverse real-world applications. Mastering this conversion, along with understanding the broader implications of decimal representation, is critical for success in mathematics and various related fields. Remember to practice different methods and explore further concepts to deepen your understanding and solidify your skills in numerical manipulation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 And 3/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.