5 Is 20 Of What Number
News Co
Apr 13, 2025 · 4 min read
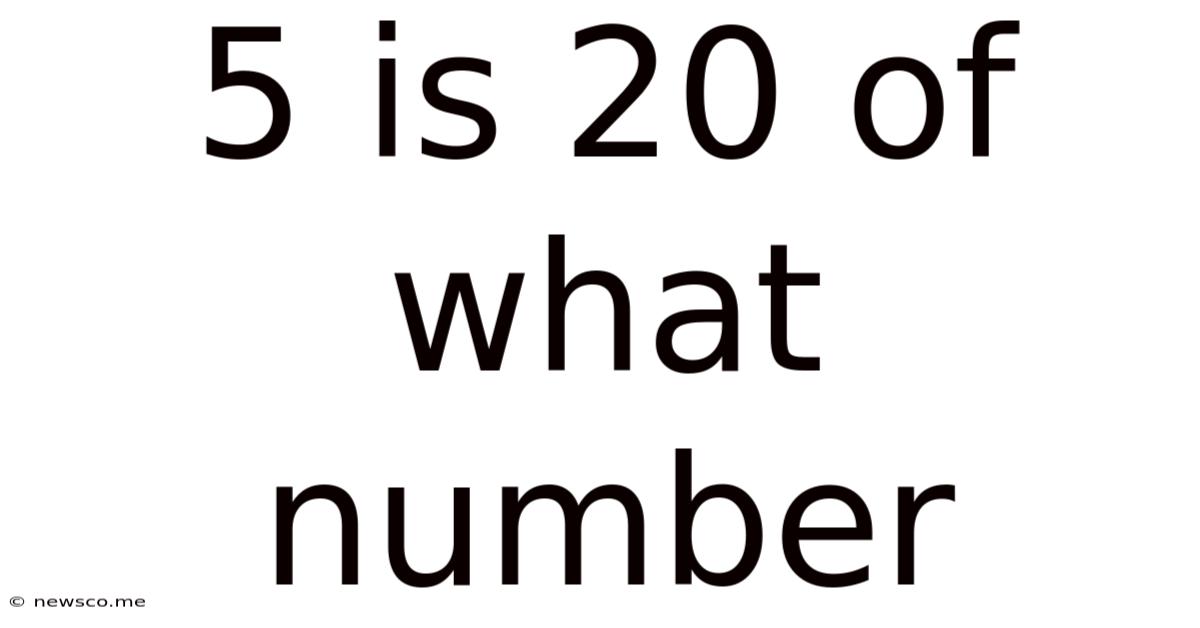
Table of Contents
5 is 20% of What Number? Unlocking the Power of Percentages
Percentages are fundamental to everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. One common type of percentage problem involves finding the whole number when a percentage of that number is known. This article will delve into solving the classic problem: "5 is 20% of what number?" We'll explore various methods to find the solution, and then broaden our understanding to tackle similar percentage problems with confidence. We'll also discuss the practical applications of these skills and resources available for further learning.
Understanding the Problem: 5 is 20% of What Number?
Before diving into the solutions, let's dissect the problem statement: "5 is 20% of what number?" This sentence translates into a mathematical equation. Let's represent the unknown number with the variable 'x'. The problem can then be expressed as:
5 = 0.20 * x
This equation states that 5 is equal to 20% (expressed as 0.20 in decimal form) of an unknown number 'x'. Our goal is to solve for 'x'.
Method 1: Using the Equation Directly
This is the most straightforward approach. We have the equation:
5 = 0.20 * x
To isolate 'x', we'll divide both sides of the equation by 0.20:
x = 5 / 0.20
x = 25
Therefore, 5 is 20% of 25.
Method 2: The Proportion Method
Proportions provide another effective way to solve percentage problems. A proportion is a statement that two ratios are equal. We can set up a proportion using the given information:
5/x = 20/100
This proportion states that the ratio of 5 (the given part) to the unknown whole (x) is equal to the ratio of 20 (the given percentage) to 100 (the whole percentage).
To solve for x, we can cross-multiply:
5 * 100 = 20 * x
500 = 20x
Now, divide both sides by 20:
x = 500 / 20
x = 25
Again, we find that 5 is 20% of 25.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100% = Percentage
In our problem, we know the part (5) and the percentage (20%). We need to find the whole (x). Rearranging the formula to solve for the whole gives us:
Whole = (Part / Percentage) * 100
Substituting the known values:
Whole = (5 / 20) * 100
Whole = 0.25 * 100
Whole = 25
Once more, we confirm that 5 is 20% of 25.
Expanding Our Understanding: Solving Similar Percentage Problems
The methods outlined above are applicable to a wide range of percentage problems. Let's consider some variations:
Example 1: Finding the Percentage
What percentage of 30 is 15?
Using the percentage formula:
(Part / Whole) * 100% = Percentage
(15 / 30) * 100% = 50%
Therefore, 15 is 50% of 30.
Example 2: Finding the Part
10% of what number is 7?
Let x represent the unknown number. The equation becomes:
0.10 * x = 7
x = 7 / 0.10
x = 70
Therefore, 10% of 70 is 7.
Example 3: Real-world Application: Sales Discounts
A store offers a 25% discount on an item originally priced at $80. What is the discount amount?
Discount amount = 25% of $80
Discount amount = 0.25 * $80
Discount amount = $20
The discount amount is $20.
Practical Applications of Percentage Calculations
The ability to solve percentage problems is crucial in many aspects of life:
- Finance: Calculating interest rates, loan payments, investment returns, and taxes.
- Retail: Determining discounts, sales tax, and profit margins.
- Science: Expressing experimental results, analyzing statistical data, and understanding proportions in various fields.
- Everyday Life: Calculating tips, splitting bills, and understanding proportions in recipes.
Resources for Further Learning
While the methods described above are comprehensive, numerous resources are available for further exploration:
- Online Calculators: Many websites offer free percentage calculators that can quickly solve various percentage problems. These can be useful for checking your work or for quick calculations.
- Khan Academy: This online learning platform provides free video tutorials and practice exercises on percentages and other mathematical concepts.
- Textbooks and Workbooks: Mathematics textbooks and workbooks dedicated to percentages and basic algebra provide a systematic approach to learning and practicing percentage calculations.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a valuable skill applicable across many disciplines. By mastering the methods discussed in this article—direct equation solving, the proportion method, and the percentage formula—you'll be equipped to confidently tackle various percentage problems. Remember to practice regularly and utilize available resources to solidify your understanding. The ability to work fluently with percentages will not only enhance your mathematical skills but also improve your ability to analyze data, make informed decisions, and succeed in various aspects of life. From simple everyday tasks to complex financial calculations, a strong grasp of percentages empowers you with valuable problem-solving capabilities. So continue practicing, and soon you'll be a percentage pro!
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.