5 Is What Percent Of 100
News Co
Apr 20, 2025 · 4 min read
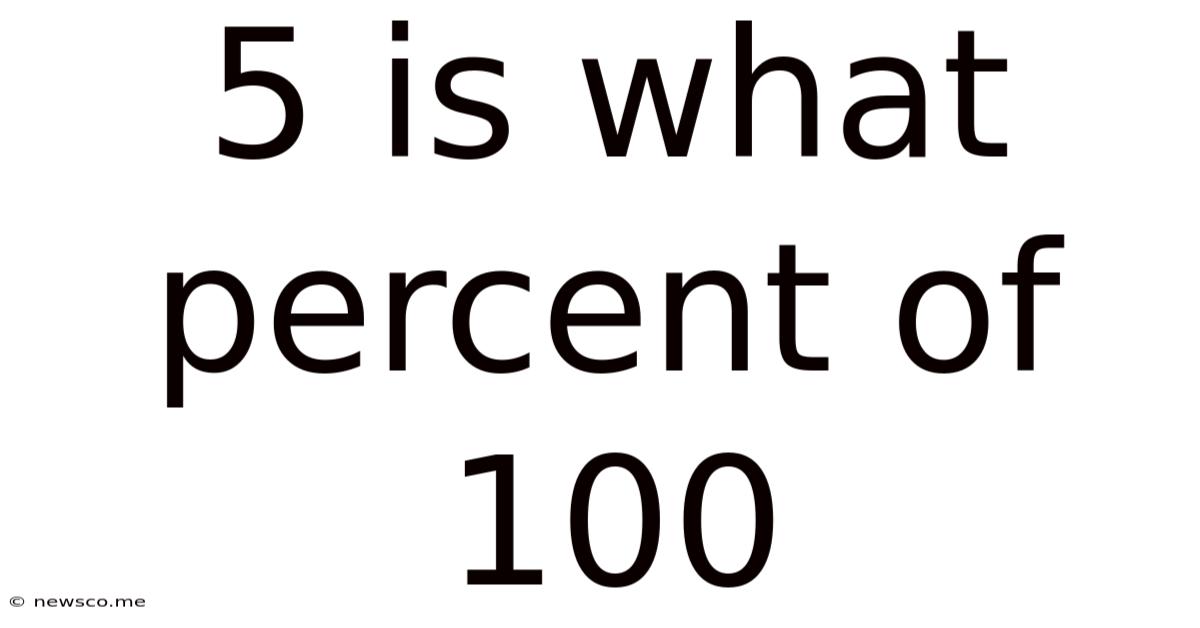
Table of Contents
5 Is What Percent of 100: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into the question, "5 is what percent of 100?", providing not only the answer but also a detailed explanation of the underlying mathematical principles and various methods for solving similar percentage problems. We'll explore different approaches, including the formula method, the proportion method, and practical applications. By the end, you'll be confident in tackling any percentage calculation.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." So, 5% means 5 out of 100, or 5/100. This fractional representation is crucial for understanding percentage calculations.
Method 1: The Formula Method
The most straightforward method for solving "5 is what percent of 100?" involves using a simple percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 5
- Whole: 100
Substituting these values into the formula:
(5 / 100) x 100% = 5%
Therefore, 5 is 5% of 100.
Method 2: The Proportion Method
The proportion method offers an alternative approach, particularly useful for visualizing the relationship between the parts and the whole. We can set up a proportion:
5 / 100 = x / 100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
5 * 100 = 100 * x
500 = 100x
x = 500 / 100
x = 5
Therefore, 5 is 5% of 100. This method clearly demonstrates the equivalence between the fraction 5/100 and the percentage 5%.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in numerous everyday situations. Here are some examples demonstrating the practical application of solving problems similar to "5 is what percent of 100?":
1. Discount Calculations:
Imagine a store offering a discount on an item originally priced at $100. If the discount is $5, what percentage discount is being offered? Using the formula:
(5 / 100) x 100% = 5%
The store is offering a 5% discount.
2. Tax Calculations:
Suppose a sales tax of $5 is added to a $100 purchase. What is the sales tax percentage? Again, using the formula:
(5 / 100) x 100% = 5%
The sales tax is 5%.
3. Grade Calculation:
A student scores 5 points out of a possible 100 points on a test. What percentage did the student score?
(5 / 100) x 100% = 5%
The student scored 5%.
4. Analyzing Survey Results:
In a survey of 100 people, 5 responded positively to a particular question. What percentage of respondents gave a positive response?
(5 / 100) x 100% = 5%
5% of respondents gave a positive response.
5. Financial Investments:
If an investment of $100 yields a profit of $5, what is the percentage return on investment (ROI)?
(5 / 100) x 100% = 5%
The ROI is 5%.
Solving More Complex Percentage Problems
While "5 is what percent of 100?" provides a straightforward example, let's explore how to adapt these methods to solve more complex percentage problems:
Example 1: Finding the Part
What is 20% of 50?
Here, we know the percentage (20%) and the whole (50). We need to find the part. We can rearrange the formula:
(Part / Whole) x 100% = Percentage
Part = (Percentage/100%) x Whole
Part = (20/100) x 50 = 10
Therefore, 20% of 50 is 10.
Example 2: Finding the Whole
15 is 30% of what number?
Here, we know the part (15) and the percentage (30%). We need to find the whole. Rearranging the formula:
Whole = (Part / Percentage) x 100%
Whole = (15 / 30) x 100 = 50
Therefore, 15 is 30% of 50.
Percentage Increase and Decrease
Percentage calculations also extend to situations involving increases and decreases.
Example 3: Percentage Increase
A value increased from 100 to 105. What is the percentage increase?
First, find the difference: 105 - 100 = 5
Then, use the formula:
(Increase / Original Value) x 100% = Percentage Increase
(5 / 100) x 100% = 5%
The percentage increase is 5%.
Example 4: Percentage Decrease
A value decreased from 100 to 95. What is the percentage decrease?
First, find the difference: 100 - 95 = 5
Then, use the formula:
(Decrease / Original Value) x 100% = Percentage Decrease
(5 / 100) x 100% = 5%
The percentage decrease is 5%.
Using Calculators and Software
Most calculators and spreadsheet software (like Microsoft Excel or Google Sheets) have built-in functions for percentage calculations. This can significantly simplify the process, especially for more complex problems. Familiarizing yourself with these functions will streamline your work.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a vital skill with broad applications in various fields. Whether you're dealing with discounts, taxes, grades, or analyzing data, mastering percentage calculations will empower you to make informed decisions and interpret information effectively. By understanding the basic formula, the proportion method, and applying these techniques to various real-world examples, you'll become confident in tackling any percentage problem. Remember to utilize calculators and software to simplify complex calculations and enhance your efficiency. The seemingly simple question, "5 is what percent of 100?", serves as a gateway to a world of quantitative understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 Is What Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.