5 Is What Percent Of 60
News Co
Apr 25, 2025 · 5 min read
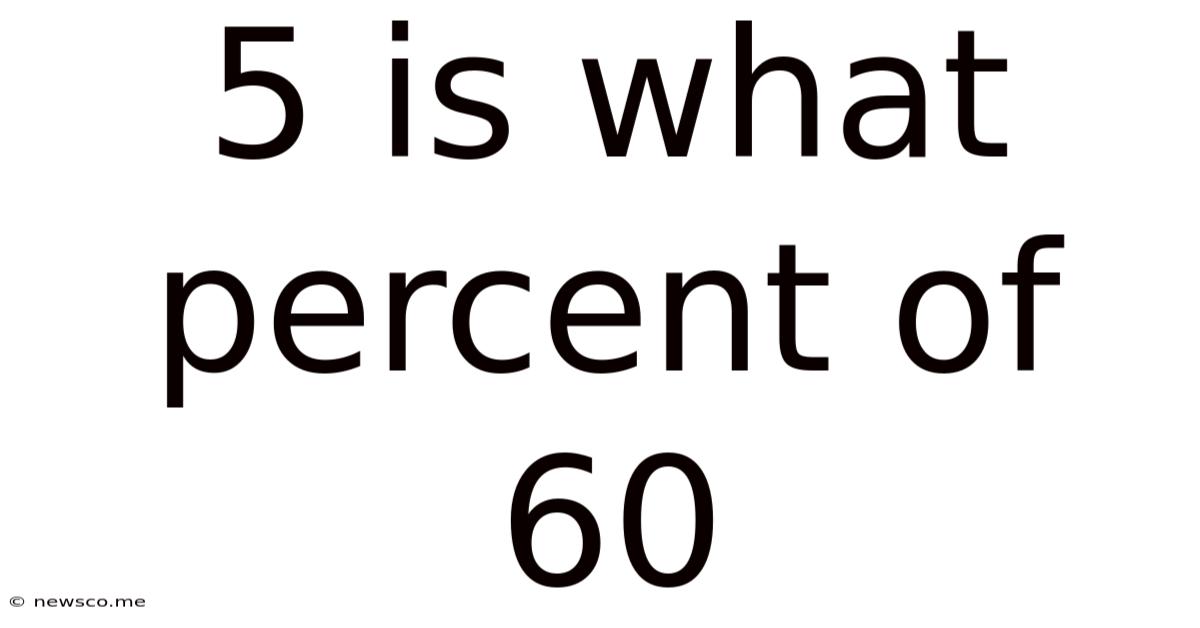
Table of Contents
5 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to interpreting statistics and analyzing data. This comprehensive guide will delve into the question, "5 is what percent of 60?", providing not just the answer but a thorough explanation of the underlying principles and various methods to solve similar percentage problems. We'll explore different approaches, including using proportions, fractions, and the simple percentage formula, ensuring a complete understanding for all readers.
Understanding Percentages: The Basics
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," indicating that the number preceding it is a portion of 100. For instance, 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
Percentages are used to express proportions and compare different quantities. They are particularly useful for showing changes or relationships between numbers. Understanding percentages is crucial in various fields, including finance, business, science, and everyday life.
Method 1: Using Proportions to Solve "5 is What Percent of 60?"
Proportions provide a straightforward method for solving percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion to find the percentage:
Part/Whole = Percent/100
In this case:
- Part: 5 (the number we're considering as a percentage of the whole)
- Whole: 60 (the total number)
- Percent: x (the unknown percentage we need to find)
Substituting these values into the proportion formula:
5/60 = x/100
To solve for x, we can cross-multiply:
5 * 100 = 60 * x
500 = 60x
Now, divide both sides by 60:
x = 500/60
x = 25/3
x ≈ 8.33
Therefore, 5 is approximately 8.33% of 60.
Method 2: Using Fractions to Solve "5 is What Percent of 60?"
We can also approach this problem using fractions. The fraction representing the relationship between 5 and 60 is 5/60. To convert this fraction to a percentage, we need to express it as a fraction with a denominator of 100:
5/60 = x/100
Cross-multiplying:
5 * 100 = 60 * x
500 = 60x
x = 500/60
x = 25/3
x ≈ 8.33
Again, we find that 5 is approximately 8.33% of 60.
Method 3: Using the Percentage Formula
The most direct method involves using the standard percentage formula:
Percentage = (Part/Whole) * 100
Substituting the values:
Percentage = (5/60) * 100
Percentage = (1/12) * 100
Percentage ≈ 8.33
This confirms that 5 is approximately 8.33% of 60.
Rounding and Accuracy
Note that in the calculations above, we obtained a result of 8.3333... This is a recurring decimal. For practical purposes, we round the percentage to a reasonable number of decimal places. Rounding to two decimal places, as done in the examples, provides sufficient accuracy for most applications. However, depending on the context, you may need to round to more or fewer decimal places.
Real-World Applications: Understanding the Significance
Understanding percentage calculations, as demonstrated by solving "5 is what percent of 60?", has numerous real-world applications:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins. For example, if a store offers a discount of 8.33% on an item originally priced at $60, the discount amount would be approximately $5.
-
Statistics: Interpreting data and presenting information in a clear and concise manner. Percentages allow for easy comparison of different datasets.
-
Science: Expressing concentrations, experimental results, and measurement errors.
-
Everyday Life: Calculating tips, comparing prices, and understanding proportions in recipes.
Expanding Your Understanding: More Complex Percentage Problems
While the example "5 is what percent of 60?" is relatively straightforward, understanding the underlying principles allows you to solve more complex percentage problems. These often involve:
-
Finding the whole: Knowing the percentage and the part, and needing to find the whole.
-
Finding the part: Knowing the percentage and the whole, and needing to find the part.
-
Percentage change: Calculating the percentage increase or decrease between two numbers.
-
Compound percentages: Calculating percentages on percentages, often seen in interest calculations.
Mastering these techniques empowers you to confidently tackle a wide array of percentage-related challenges.
Practical Exercises: Testing Your Knowledge
To solidify your understanding, try solving these problems:
- 12 is what percent of 48?
- What is 20% of 150?
- If a price increases from $50 to $60, what is the percentage increase?
- A shirt is discounted by 15% and now costs $34. What was the original price?
These exercises will allow you to apply the methods discussed and further enhance your understanding of percentage calculations. Remember to approach each problem systematically, using either proportions, fractions, or the percentage formula. Accurate calculations are vital, so double-check your work!
Conclusion: Mastering Percentages for Success
The ability to solve percentage problems, such as determining "5 is what percent of 60?", is a valuable skill with applications across numerous areas of life. By understanding the fundamental principles and mastering the different calculation methods, you equip yourself with a powerful tool for solving various mathematical challenges and interpreting real-world data. Consistent practice and application will further hone your skills, allowing you to confidently handle percentage problems of increasing complexity. Remember that understanding percentages is not just about solving equations; it's about interpreting data, making informed decisions, and navigating the numerical world with greater confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.