5 Is What Percentage Of 8
News Co
Mar 19, 2025 · 5 min read
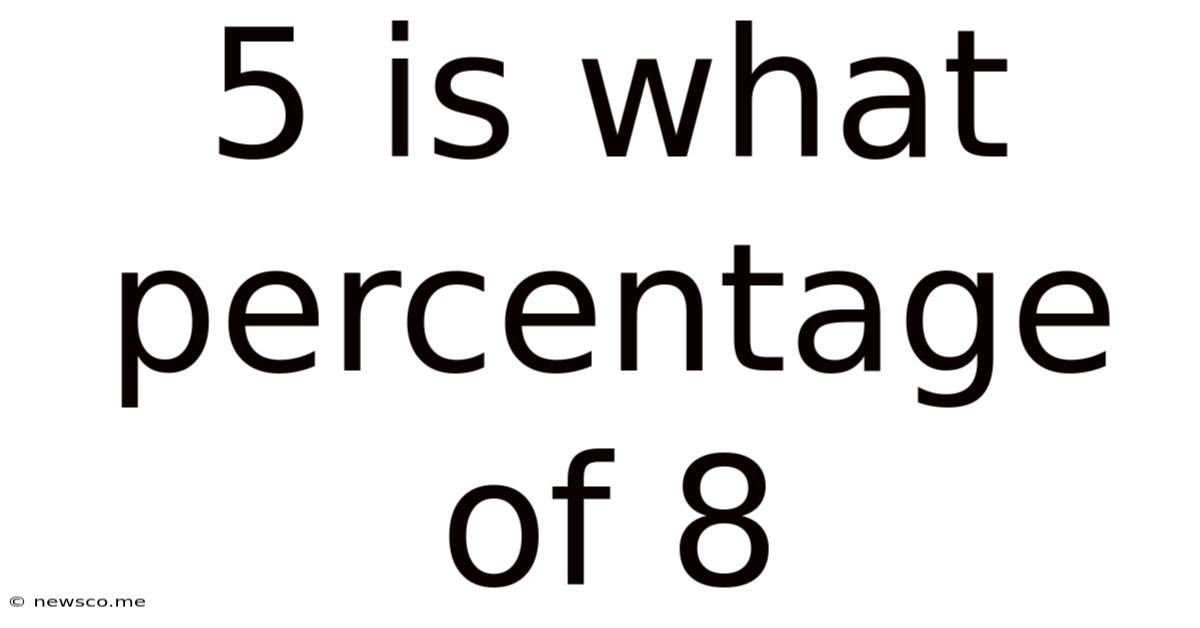
Table of Contents
5 is What Percentage of 8? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and taxes to comprehending statistics and financial data. This article delves into the seemingly simple question, "5 is what percentage of 8?", providing a thorough explanation of the calculation process, exploring different methods, and offering practical applications to solidify your understanding. We'll also examine related concepts and address common misconceptions surrounding percentage calculations.
Understanding the Basics: What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Percentages are used to represent proportions or ratios, making it easier to compare different quantities or values. For example, 50% represents 50 out of 100, or one-half.
Calculating "5 is What Percentage of 8?"
The core of solving this problem lies in understanding the relationship between the part (5), the whole (8), and the percentage we're trying to find. We can approach this calculation using two primary methods:
Method 1: Using the Formula
The most straightforward method is using the percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 5
- Whole: 8
Substituting these values into the formula:
(5 / 8) x 100% = 0.625 x 100% = 62.5%
Therefore, 5 is 62.5% of 8.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion:
Part / Whole = Percentage / 100
Again, we know:
- Part: 5
- Whole: 8
Substituting:
5 / 8 = x / 100
To solve for 'x' (the percentage), we cross-multiply:
8x = 500
x = 500 / 8
x = 62.5
Therefore, 5 is 62.5% of 8.
Practical Applications: Real-World Examples
Understanding percentage calculations isn't just an academic exercise; it's a crucial skill for navigating everyday situations. Here are a few examples:
-
Discounts: Imagine a shirt originally priced at $8 is on sale for $5. Using the methods above, we've determined that the discount is 62.5%.
-
Grades: If you scored 5 out of 8 points on a quiz, your percentage score is 62.5%.
-
Surveys and Statistics: In market research, if 5 out of 8 respondents prefer a certain product, the preference rate is 62.5%.
-
Financial Calculations: Calculating interest rates, returns on investments, or profit margins often involves percentage calculations.
-
Data Analysis: Representing data as percentages allows for easy comparison and interpretation, even when dealing with vastly different sample sizes.
Extending the Understanding: Variations and Related Concepts
Let's explore some related concepts and variations to deepen your grasp of percentage calculations:
Finding the Whole when the Percentage and Part are Known
Suppose you know that 62.5% of a certain number is 5. How do you find the whole number? We can modify the formula:
Whole = (Part / Percentage) x 100
Substituting:
Whole = (5 / 62.5) x 100 = 8
This confirms our original calculation.
Finding the Part when the Percentage and Whole are Known
If we know that 62.5% of 8 is what number, we can use a different variation:
Part = (Percentage / 100) x Whole
Substituting:
Part = (62.5 / 100) x 8 = 5
This reinforces our understanding of the relationships between the parts and the whole.
Dealing with Decimals and Fractions in Percentage Calculations
Percentages can involve decimals or fractions. For example, if 5 is what percentage of 7.5, the calculation is:
(5 / 7.5) x 100% ≈ 66.67%
Similarly, if you need to find what percentage 2/3 is of 1, the calculation becomes:
(2/3 / 1) x 100% ≈ 66.67%
The process remains the same; you simply perform the division first, before multiplying by 100%.
Common Mistakes to Avoid
Several common errors can lead to inaccurate percentage calculations. Let's address some of them:
-
Incorrect Formula Application: Using the wrong formula or misplacing values within the formula is a frequent mistake. Always double-check your work.
-
Order of Operations: Remember the order of operations (PEMDAS/BODMAS): parentheses/brackets, exponents/orders, multiplication and division (from left to right), addition and subtraction (from left to right).
-
Decimal Point Errors: Incorrect placement of the decimal point during multiplication or division can drastically alter the result.
-
Confusing Part and Whole: Make sure to identify the part and the whole correctly before applying the formula. The context of the problem is key.
-
Rounding Errors: While rounding is sometimes necessary, be aware that excessive rounding can introduce inaccuracies into your final answer.
Improving your Percentage Calculation Skills
Mastering percentage calculations is a process that requires practice. Here are some tips for improvement:
-
Practice Regularly: Work through a variety of problems, starting with simple ones and gradually increasing the complexity.
-
Use Multiple Methods: Try solving the same problem using different methods to verify your results and develop a deeper understanding.
-
Real-World Application: Apply percentage calculations to real-life situations to reinforce your learning and make it more relevant.
-
Utilize Online Resources: There are many online resources, including calculators and interactive exercises, that can help you improve your skills.
Conclusion: The Power of Percentage Understanding
Understanding percentages is a versatile and indispensable skill. By mastering the fundamental concepts and applying the methods outlined in this article, you can confidently solve percentage-related problems in various contexts. Remember to practice regularly, watch out for common mistakes, and apply your knowledge to real-world situations to strengthen your proficiency. The seemingly simple question of "5 is what percentage of 8?" opens a door to a broader understanding of numerical relationships and their practical applications in everyday life and professional pursuits. This comprehensive guide provides a strong foundation for tackling more complex percentage problems and confidently navigating the numerical world around us.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 5 Is What Percentage Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.