5 Percent As A Fraction In Simplest Form
News Co
Mar 30, 2025 · 5 min read
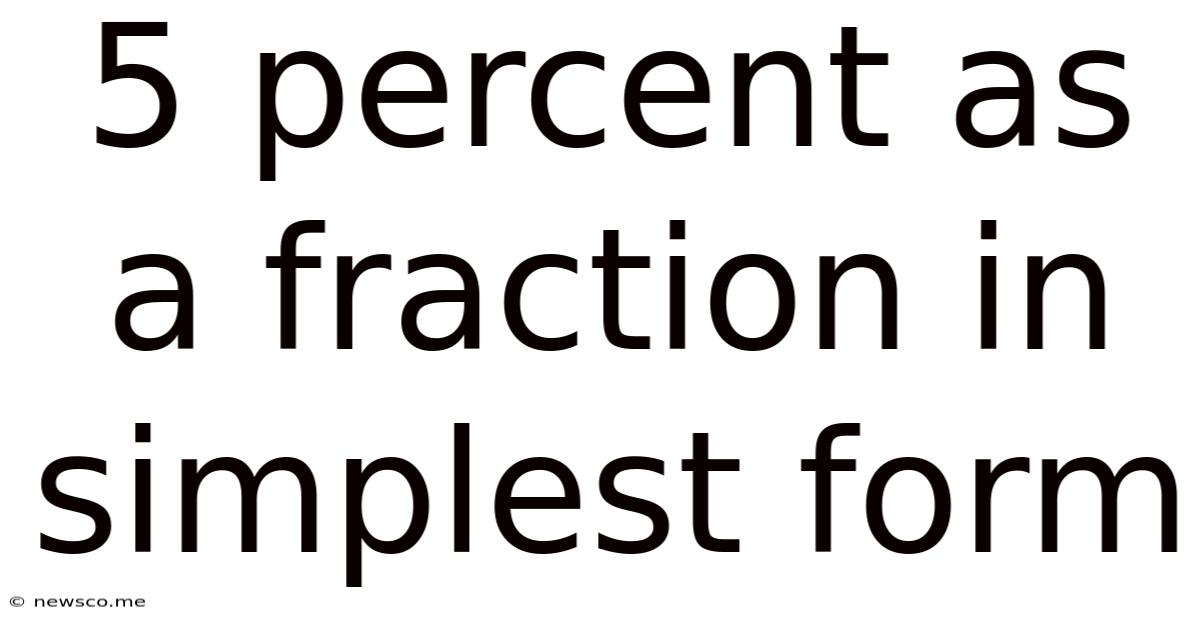
Table of Contents
5 Percent as a Fraction in Simplest Form: A Comprehensive Guide
Understanding percentages, fractions, and decimals is fundamental to various aspects of life, from calculating discounts and taxes to comprehending financial reports and statistical data. This comprehensive guide delves into the conversion of percentages to fractions, specifically focusing on expressing 5 percent as a fraction in its simplest form. We'll explore the underlying concepts, demonstrate the conversion process step-by-step, and provide numerous examples to solidify your understanding.
Understanding Percentages and Fractions
Before diving into the conversion, let's review the basic definitions:
-
Percentage: A percentage represents a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). So, 5% means 5 out of 100.
-
Fraction: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction ½, 1 is the numerator and 2 is the denominator.
The key to converting percentages to fractions lies in understanding that the percentage can be directly written as a fraction with a denominator of 100.
Converting 5 Percent to a Fraction
The conversion of 5% to a fraction follows these simple steps:
-
Write the percentage as a fraction with a denominator of 100:
5% = 5/100
-
Simplify the fraction: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In this case, the GCD of 5 and 100 is 5.
-
Divide both the numerator and the denominator by the GCD:
5 ÷ 5 = 1 100 ÷ 5 = 20
-
Express the simplified fraction:
Therefore, 5% as a fraction in its simplest form is 1/20.
Illustrative Examples: Expanding the Concept
Let's expand on this concept with more examples, showcasing the versatility of percentage-to-fraction conversion. Understanding these examples will solidify your understanding and equip you to handle similar conversions independently.
Example 1: Calculating a Discount
A store offers a 5% discount on all items. If an item costs $100, what is the discount amount in dollars?
-
Step 1: Convert the percentage to a fraction: 5% = 1/20
-
Step 2: Multiply the original price by the fraction: $100 * (1/20) = $5
The discount amount is $5.
Example 2: Portion of a Whole
A class has 20 students. 5% of the students are absent. How many students are absent?
-
Step 1: Convert the percentage to a fraction: 5% = 1/20
-
Step 2: Multiply the total number of students by the fraction: 20 students * (1/20) = 1 student
One student is absent.
Example 3: Understanding Proportions
A recipe calls for 5% vinegar in a total volume of 200ml. How many ml of vinegar are needed?
-
Step 1: Convert the percentage to a fraction: 5% = 1/20
-
Step 2: Multiply the total volume by the fraction: 200ml * (1/20) = 10ml
10ml of vinegar are needed.
Example 4: Working with Larger Numbers
A company reports a 5% increase in profit, which was initially $500,000. What is the increase in profit?
-
Step 1: Convert the percentage to a fraction: 5% = 1/20
-
Step 2: Multiply the initial profit by the fraction: $500,000 * (1/20) = $25,000
The increase in profit is $25,000.
These examples demonstrate the practical applications of converting percentages to fractions. This conversion is crucial for solving various real-world problems accurately.
Advanced Applications and Related Concepts
The ability to convert percentages to fractions opens doors to more complex mathematical operations and problem-solving. Here are a few advanced applications and related concepts:
Combining Percentages and Fractions in Calculations
Often, you will need to combine percentages and fractions within a single calculation. For example, you might need to calculate a discount (a percentage) on an item that is already discounted (fractional reduction). This requires proficiency in handling both forms.
Working with Compound Percentages
Compound percentages involve applying a percentage to a value, then applying another percentage to the resulting value. Converting percentages to fractions can simplify these calculations.
Probability and Statistics
In probability and statistics, percentages are frequently used to represent the likelihood of an event occurring. Understanding the fractional equivalent provides a clearer understanding of the underlying probabilities.
Financial Modeling
Financial modeling uses percentages extensively to represent interest rates, growth rates, and various financial ratios. The ability to convert percentages to fractions is a fundamental skill for financial analysts.
Common Mistakes to Avoid
While the conversion of 5% to 1/20 is straightforward, there are common pitfalls to watch out for:
-
Forgetting to simplify: Leaving the fraction as 5/100 is incorrect; it's crucial to always simplify the fraction to its simplest form.
-
Incorrect GCD calculation: Accurately determining the greatest common divisor is vital for proper simplification.
-
Misinterpreting the percentage: Make sure to understand what the percentage represents within the context of the problem.
By avoiding these common mistakes, you'll ensure the accuracy of your calculations.
Conclusion: Mastering Percentage-to-Fraction Conversions
Converting percentages to fractions is a vital skill applicable across numerous disciplines. Mastering this skill strengthens your mathematical foundation and empowers you to tackle complex problems involving percentages, fractions, and other mathematical concepts. The conversion of 5% to its simplest fractional form, 1/20, serves as a fundamental building block for more advanced applications. Through consistent practice and careful attention to detail, you can build confidence and proficiency in handling percentage-to-fraction conversions, leading to improved accuracy and problem-solving abilities in diverse real-world scenarios. Remember to always simplify your fraction to its lowest terms for a clear and concise representation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 Percent As A Fraction In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.