50 Is 20 Percent Of What Number
News Co
May 08, 2025 · 5 min read
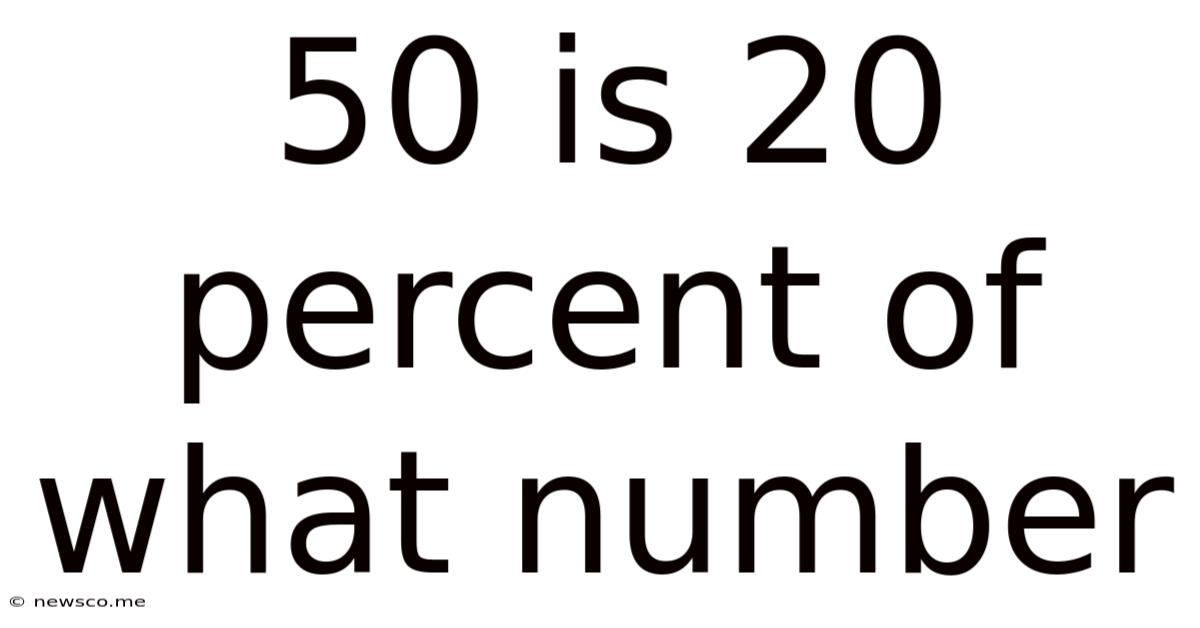
Table of Contents
50 is 20 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Finding a percentage of a number, or working backward to find the original number from a percentage, is a fundamental skill with wide-ranging applications in various aspects of life. Whether you're calculating discounts, understanding financial statements, or tackling a math problem, mastering percentage calculations is essential. This article delves deep into the question, "50 is 20 percent of what number?", explaining not only the solution but also providing a comprehensive understanding of the underlying concepts and various methods to solve similar percentage problems.
Understanding Percentages
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or a ratio expressed as a portion of 100. The symbol "%" represents "percent," meaning "per hundred." For example, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20.
Understanding this fundamental relationship is crucial for solving percentage problems. We can represent any percentage as a decimal by dividing the percentage by 100. Conversely, we can convert any decimal to a percentage by multiplying it by 100.
Method 1: Using the Equation Method
This method is arguably the most straightforward and widely applicable approach to solving percentage problems. We can express the problem mathematically as an equation:
Part = Percentage × Whole
In our problem, "50 is 20 percent of what number?", we know the following:
- Part: 50 (this is the portion we're given)
- Percentage: 20% (or 0.20 as a decimal)
- Whole: This is the unknown number we need to find; let's represent it with 'x'.
Substituting these values into our equation, we get:
50 = 0.20 × x
To solve for x, we simply divide both sides of the equation by 0.20:
x = 50 / 0.20
x = 250
Therefore, 50 is 20 percent of 250.
Method 2: Using Proportions
The proportion method offers an alternative approach to solving percentage problems. It leverages the concept of equivalent ratios. We can set up a proportion as follows:
Part / Whole = Percentage / 100
Using the information from our problem:
50 / x = 20 / 100
To solve for x, we cross-multiply:
50 × 100 = 20 × x
5000 = 20x
Now, divide both sides by 20:
x = 5000 / 20
x = 250
Again, we find that 50 is 20 percent of 250.
Method 3: Using the Percentage Formula Rearrangement
This method involves directly rearranging the basic percentage formula to solve for the "whole" or the original number. Starting with the standard formula:
Percentage = (Part / Whole) × 100
We want to solve for the "Whole," so we need to rearrange the formula:
Whole = (Part / Percentage) × 100
Plugging in our values:
Whole = (50 / 20) × 100
Whole = 2.5 × 100
Whole = 250
This method confirms that 50 is 20 percent of 250.
Real-World Applications of Percentage Calculations
Understanding percentage calculations extends far beyond mathematical exercises. Here are some real-world examples where this skill is invaluable:
1. Financial Calculations:
- Discounts: Calculating sale prices based on percentage discounts is a common application. If a store offers a 20% discount on a $250 item, the discount amount would be 20% of $250, which is $50, resulting in a sale price of $200.
- Interest Rates: Understanding interest rates on loans, mortgages, and savings accounts requires percentage calculations. The interest accrued is a percentage of the principal amount.
- Taxes: Calculating sales tax, income tax, and other taxes often involves determining a percentage of an amount.
- Investment Returns: Tracking the percentage increase or decrease in investment value is crucial for financial planning.
- Profit Margins: Businesses calculate their profit margins as a percentage of their revenue to understand profitability.
2. Everyday Life Applications:
- Tip Calculation: Calculating tips in restaurants is often done as a percentage of the total bill.
- Grade Calculation: Many grading systems use percentages to represent a student's performance.
- Survey Results: Analyzing survey results frequently involves representing responses as percentages of the total number of respondents.
- Cooking and Baking: Recipes sometimes use percentages to indicate the proportion of ingredients.
- Sports Statistics: Many sports statistics, such as batting averages and field goal percentages, are expressed as percentages.
3. Scientific and Research Applications:
- Data Analysis: Scientists use percentage calculations extensively for data analysis and interpretation.
- Statistical Significance: Researchers use percentages to determine the statistical significance of their results.
Expanding Your Percentage Calculation Skills
Mastering percentage calculations is an iterative process. Practice is key to improving your speed and accuracy. Here are some ways to expand your skills:
- Solve a variety of percentage problems: Try different types of problems, including finding the percentage of a number, finding what percentage one number is of another, and finding the original number from a given percentage.
- Use different methods: Familiarize yourself with the various methods (equation method, proportion method, rearrangement of formula) and choose the method that suits your problem-solving style best.
- Check your work: Always verify your calculations to ensure accuracy. Use a calculator or different method to cross-check your results.
- Seek additional resources: There are numerous online resources, tutorials, and practice problems available to help you improve your skills. Look for websites, videos, or educational materials that focus on percentage calculations.
Conclusion
This article has comprehensively addressed the question, "50 is 20 percent of what number?", providing not only the answer (250) but also detailed explanations of three different calculation methods and numerous real-world applications. Remember, understanding percentages is a fundamental skill that is broadly applicable across diverse fields. By mastering these concepts and practicing regularly, you'll develop a valuable skillset applicable to many facets of life. Continued practice and exploration of various problem types will solidify your understanding and make you a more confident and efficient percentage calculator.
Latest Posts
Latest Posts
-
Integer Addition And Subtraction Word Problems
May 09, 2025
-
What Are The Prime Numbers Of 34
May 09, 2025
-
Find The Quotient Of 9 10 And 2 3
May 09, 2025
-
How Do You Find The Diameter Of A Rectangle
May 09, 2025
-
How Many Weeks Are In 25 Days
May 09, 2025
Related Post
Thank you for visiting our website which covers about 50 Is 20 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.