50 Is 25 Of What Number
News Co
Apr 21, 2025 · 5 min read
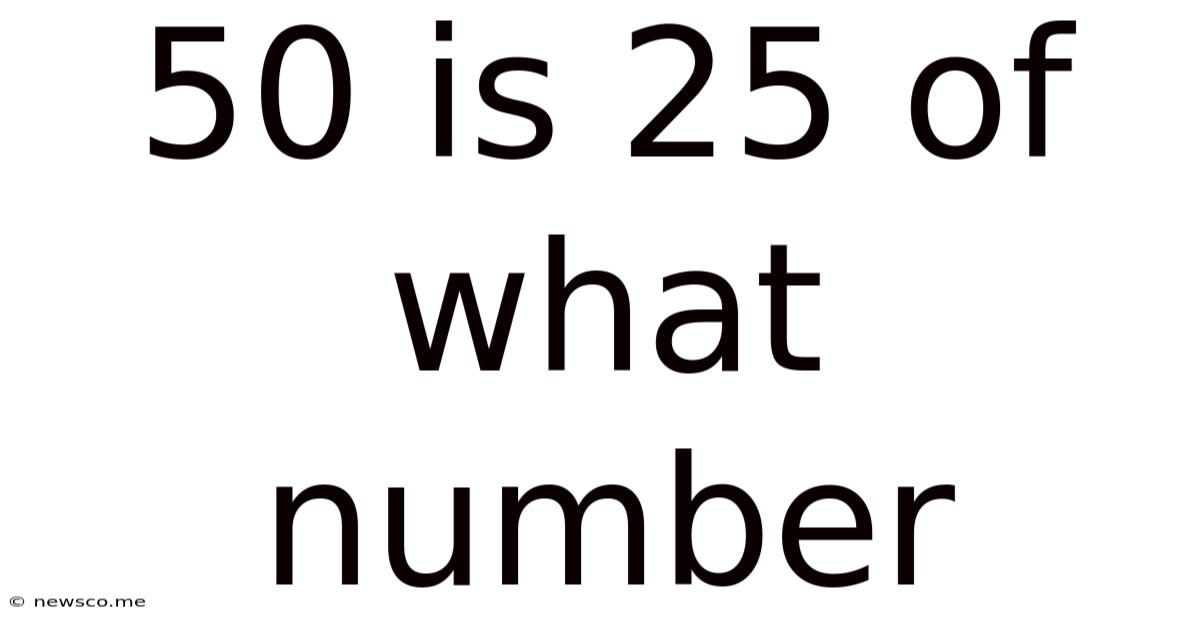
Table of Contents
50 is 25% of What Number? Unraveling Percentage Problems
This seemingly simple question, "50 is 25% of what number?", opens the door to a broader understanding of percentages and their application in various real-world scenarios. While the solution might seem straightforward, exploring the different methods of solving it reveals fundamental mathematical concepts and practical problem-solving strategies. This article will not only provide the answer but will also delve into the underlying principles, equipping you with the tools to tackle similar percentage problems confidently.
Understanding Percentages: The Foundation
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
This fractional representation is crucial in solving percentage problems. Understanding this equivalence allows us to easily translate percentages into fractions and decimals, and vice-versa, enabling flexible approaches to problem-solving.
Method 1: Using the Percentage Formula
The most direct way to solve "50 is 25% of what number?" is by using the standard percentage formula:
Part = Percentage × Whole
In this equation:
- Part: Represents the portion of the whole we're dealing with (in this case, 50).
- Percentage: The rate expressed as a decimal or fraction (25% = 0.25 or 25/100).
- Whole: The total quantity we're trying to find.
Let's substitute the known values into the formula:
50 = 0.25 × Whole
To isolate the "Whole," we need to divide both sides of the equation by 0.25:
Whole = 50 / 0.25
Whole = 200
Therefore, 50 is 25% of 200.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can represent the problem as:
50/x = 25/100
Here:
- 50 represents the "part".
- x represents the "whole" we need to find.
- 25/100 represents the percentage as a fraction.
To solve for x, we can cross-multiply:
50 × 100 = 25 × x
5000 = 25x
Now, divide both sides by 25:
x = 5000 / 25
x = 200
Again, the answer is 200. This method reinforces the concept of equivalent ratios and provides an alternative approach to solving percentage problems.
Method 3: Working Backwards from the Percentage
Since 25% represents one-quarter (25/100 = 1/4), we can also solve the problem by considering that 50 is one-quarter of the unknown number. To find the whole number, we simply multiply 50 by 4:
50 × 4 = 200
This approach utilizes the intuitive understanding of percentages and their fractional equivalents. It's a quicker method suitable for problems involving easily identifiable fractions like 25%, 50%, and 75%.
Practical Applications: Real-World Scenarios
Understanding how to solve percentage problems like "50 is 25% of what number?" has far-reaching applications in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, tax amounts, and profit margins all rely on percentage calculations. For instance, if you receive a 25% discount on a $200 item, you would save $50.
-
Sales and Marketing: Tracking sales performance, analyzing market share, and setting sales targets often involve percentages. Understanding the relationship between sales figures and percentage growth is essential for strategic decision-making.
-
Science and Engineering: Percentages are widely used in scientific studies to express probabilities, uncertainties, and experimental errors. Data analysis and interpretation often rely on percentage representations.
-
Everyday Life: Calculating tips at restaurants, understanding discount offers, or determining the percentage of completion of a task all involve applying percentage calculations.
Advanced Percentage Problems: Building Your Skills
While the problem "50 is 25% of what number?" provides a foundational understanding of percentage calculations, it's crucial to expand your skills to handle more complex scenarios. Here are some examples of more advanced problems:
Problem 1: A store offers a 15% discount on an item originally priced at $120. What is the discounted price?
Solution: First, calculate the discount amount: 15% of $120 = 0.15 × $120 = $18. Then, subtract the discount from the original price: $120 - $18 = $102. The discounted price is $102.
Problem 2: If the price of a product increased from $50 to $60, what is the percentage increase?
Solution: Calculate the difference in price: $60 - $50 = $10. Then, divide the difference by the original price and multiply by 100%: ($10/$50) × 100% = 20%. The percentage increase is 20%.
Problem 3: A salesperson earns a 5% commission on all sales. If their commission for the month was $250, what was their total sales for the month?
Solution: Let 'x' be the total sales. The equation would be: 0.05x = $250. Solving for x, we get: x = $250 / 0.05 = $5000. Their total sales were $5000.
Mastering Percentages: Continuous Learning
Developing proficiency in percentage calculations involves consistent practice and the exploration of different problem-solving approaches. Start with simpler problems like "50 is 25% of what number?" to build your foundational understanding. Then gradually increase the complexity of the problems you tackle, incorporating real-world scenarios to make the learning process more engaging and relevant. Remember, the more you practice, the more confident and adept you will become at solving percentage problems of all kinds. This will not only improve your mathematical abilities but will also equip you with a valuable skill applicable across many aspects of life.
Latest Posts
Related Post
Thank you for visiting our website which covers about 50 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.