50 Is 40 Percent Of What
News Co
May 08, 2025 · 5 min read
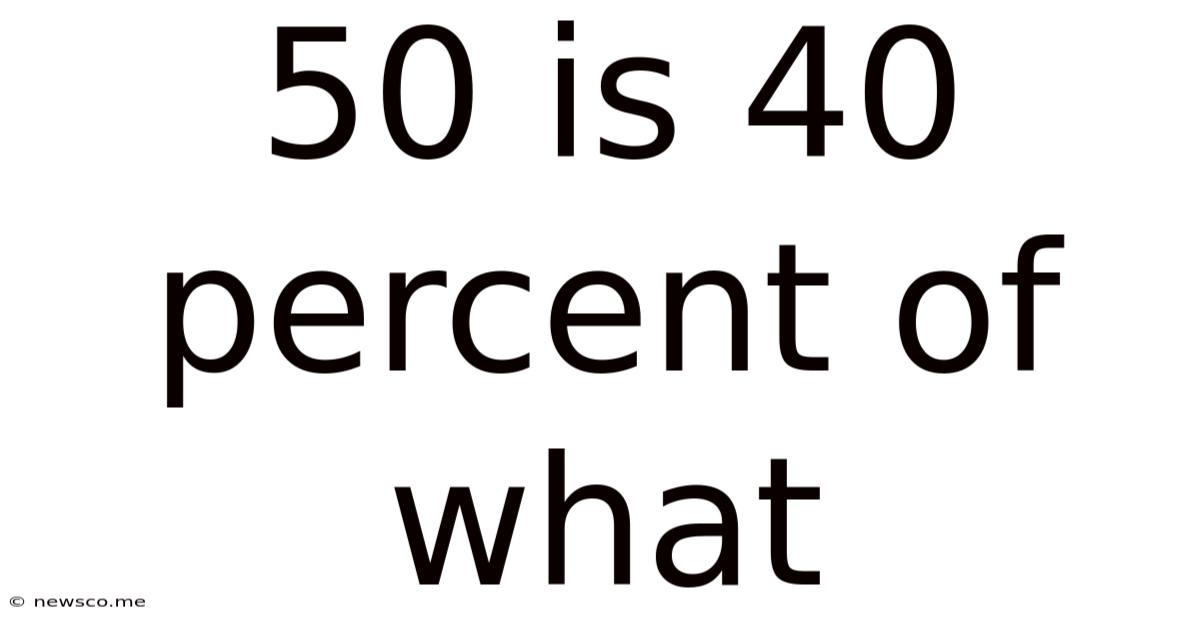
Table of Contents
50 is 40 Percent of What? A Comprehensive Guide to Percentage Calculations
Finding out what number 50 represents 40% of involves understanding and applying percentage calculations. This seemingly simple question unlocks a world of practical applications across various fields, from everyday budgeting to complex financial modeling. This comprehensive guide will not only answer the question directly but also delve into the underlying principles, provide various solution methods, and explore real-world examples to solidify your understanding.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For instance, 40% means 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40.
Solving: 50 is 40 Percent of What?
The problem "50 is 40% of what?" can be expressed mathematically as:
50 = 0.40 * x
where 'x' is the unknown number we're trying to find. To solve for 'x', we need to isolate it on one side of the equation.
Method 1: Algebraic Solution
-
Rewrite the equation: 50 = 0.40x
-
Divide both sides by 0.40: 50 / 0.40 = x
-
Calculate: x = 125
Therefore, 50 is 40% of 125.
Method 2: Using Proportions
Proportions offer another way to solve percentage problems. We can set up a proportion as follows:
40/100 = 50/x
This reads as "40 is to 100 as 50 is to x." To solve:
-
Cross-multiply: 40 * x = 50 * 100
-
Simplify: 40x = 5000
-
Divide by 40: x = 5000 / 40
-
Calculate: x = 125
Again, we find that 50 is 40% of 125.
Method 3: The Percentage Formula
A more general formula for percentage problems is:
(Part / Whole) * 100% = Percentage
In our case, we know the "Part" (50) and the "Percentage" (40%). We need to find the "Whole" (x). Rearranging the formula to solve for the whole:
Whole = (Part / Percentage) * 100
Substituting our values:
x = (50 / 40) * 100
x = 1.25 * 100
x = 125
This confirms, once more, that 50 is 40% of 125.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
1. Finance and Budgeting
- Calculating discounts: If a store offers a 40% discount on a $125 item, you can quickly determine the discount amount ($50) and the final price ($75).
- Analyzing investment returns: Percentage calculations are essential for tracking investment growth and understanding returns on investments. A 40% return on a $125 investment would result in a profit of $50.
- Managing personal finances: Budgeting effectively requires understanding percentages for allocating funds to different categories (e.g., 40% for housing, 20% for food, etc.).
- Calculating loan interest: Percentage calculations are used to determine the interest amount on loans, helping you understand your overall cost.
2. Business and Sales
- Analyzing market share: Companies use percentages to track their market share compared to competitors. A 40% market share means the company controls 40% of the total market.
- Calculating profit margins: Profit margins are expressed as percentages, showing the profitability of a product or service.
- Setting sales targets: Sales teams often work with percentage-based targets, aiming to increase sales by a certain percentage each year.
3. Science and Statistics
- Representing data: Percentages are commonly used to represent data visually using pie charts and bar graphs.
- Expressing probabilities: Probabilities are often expressed as percentages. For example, there's a 40% chance of rain.
4. Everyday Life
- Calculating tips: People often calculate tips as a percentage of the total bill (e.g., a 20% tip).
- Understanding sales tax: Sales tax is usually expressed as a percentage of the purchase price.
- Measuring ingredients: Cooking recipes frequently use percentages to indicate the proportion of each ingredient.
Beyond the Basics: More Complex Percentage Problems
While the problem "50 is 40% of what?" is straightforward, percentage calculations can become more complex. Here are a few examples:
- Finding the percentage increase or decrease: If a value increases from 100 to 150, the percentage increase is calculated as: [(150 - 100) / 100] * 100% = 50%. Similarly, a decrease is calculated using the same formula.
- Calculating compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This requires repeated percentage calculations.
- Solving problems involving multiple percentages: Some problems involve combining or subtracting percentages (e.g., finding the final price after successive discounts).
Mastering Percentage Calculations: Tips and Tricks
Here are a few tips to improve your percentage calculation skills:
- Practice regularly: The more you practice, the more comfortable you'll become with these calculations.
- Use different methods: Try different approaches to solving percentage problems to find the method that works best for you.
- Understand the underlying concepts: Focus on understanding the core concepts of percentages rather than just memorizing formulas.
- Use a calculator when needed: Calculators can be helpful for more complex calculations, especially those involving large numbers or multiple steps.
- Check your work: Always double-check your answers to ensure accuracy.
Conclusion
The seemingly simple question, "50 is 40 percent of what?" opens the door to a wide world of mathematical applications crucial for navigating various aspects of life. Mastering percentage calculations equips you with a fundamental skill applicable to finance, business, science, and countless everyday situations. By understanding the different methods of calculation and practicing regularly, you can build confidence and efficiency in handling percentage problems of any complexity. Remember, the key is to understand the underlying principles and choose the solution method that best suits your needs.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 50 Is 40 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.