50 Is 80 Of What Number
News Co
May 08, 2025 · 4 min read
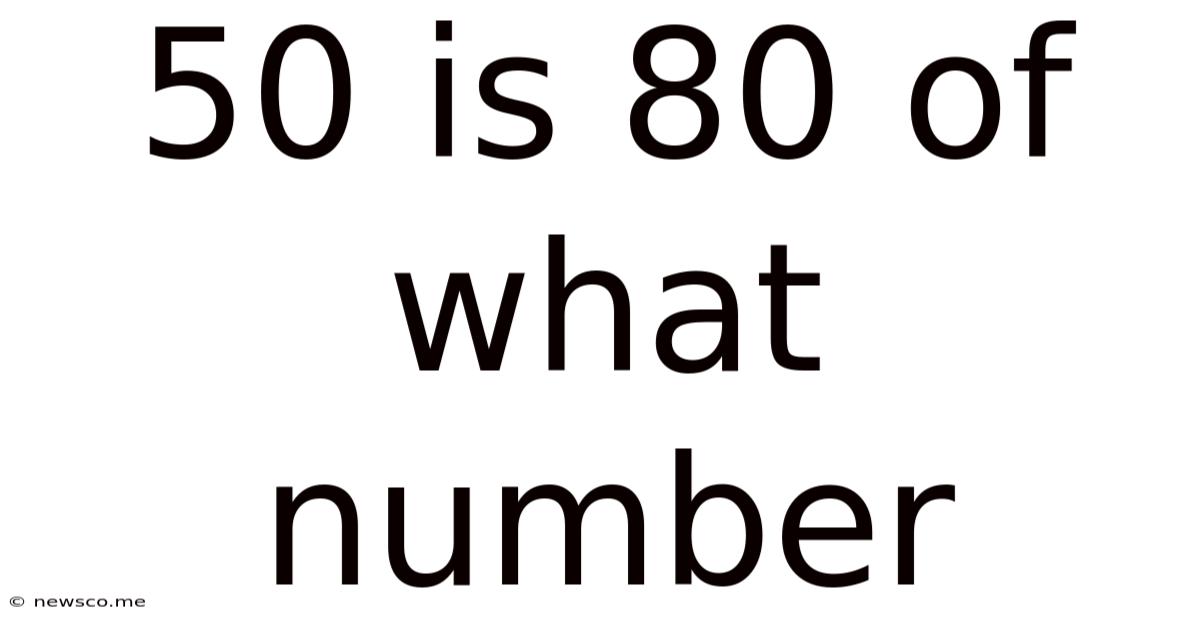
Table of Contents
50 is 80% of What Number? Unraveling Percentages and Proportions
This seemingly simple question, "50 is 80% of what number?", opens the door to a world of practical applications for percentages and proportions. Understanding how to solve this type of problem is crucial in various fields, from everyday budgeting and shopping to complex scientific calculations and financial analysis. This comprehensive guide will not only show you how to solve this specific problem but also equip you with the broader understanding needed to tackle any percentage-related calculation.
Understanding Percentages: The Foundation
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For instance, 80% means 80 out of 100, which can be written as the fraction 80/100 or the decimal 0.8. This foundational concept is key to solving percentage problems.
Method 1: Using the Equation Approach
This method directly translates the problem into a mathematical equation. We can represent the problem "50 is 80% of what number?" as follows:
50 = 0.8 * x
Where:
- 50 represents the value we're given.
- 0.8 represents 80% (converted to decimal form).
- x represents the unknown number we're trying to find.
To solve for x, we simply need to isolate it by dividing both sides of the equation by 0.8:
x = 50 / 0.8
x = 62.5
Therefore, 50 is 80% of 62.5.
Method 2: The Proportion Method
This method utilizes the concept of proportions, which are essentially two equal ratios. We can set up a proportion to solve our problem:
50/x = 80/100
Where:
- 50 represents the given value (part).
- x represents the unknown total value (whole).
- 80 represents the percentage (part).
- 100 represents the total percentage (whole).
To solve this proportion, we cross-multiply:
50 * 100 = 80 * x
5000 = 80x
Now, divide both sides by 80 to isolate x:
x = 5000 / 80
x = 62.5
Again, we arrive at the answer: 50 is 80% of 62.5.
Method 3: Using a Calculator (A Quick Approach)
For a quicker solution, especially when dealing with more complex percentage problems, you can utilize a calculator. Most calculators have a percentage function. Simply input the following:
(50 / 80) * 100
This calculation will directly give you the answer, which is 62.5.
Real-World Applications: Percentage Calculations in Everyday Life
Understanding percentage calculations isn't just about solving mathematical problems; it's a vital life skill. Here are some real-world examples where this knowledge proves invaluable:
1. Shopping and Discounts:
Imagine a shirt is on sale for 20% off its original price of $50. To find the discounted price, you'd calculate 20% of $50 (0.2 * $50 = $10) and then subtract the discount from the original price ($50 - $10 = $40). You've successfully applied percentage calculations to save money!
2. Budgeting and Finance:
When budgeting your income, you might allocate a certain percentage to savings, rent, food, and other expenses. Calculating these percentages ensures you stay on track financially. Similarly, understanding interest rates, which are expressed as percentages, is crucial for managing loans and investments.
3. Tax Calculations:
Sales tax, income tax, and property tax are all calculated as percentages. Knowing how to compute these percentages is essential for accurately determining your tax obligations.
4. Grade Calculations:
In educational settings, your final grade is often calculated based on the weighted average of various assignments and exams, which are frequently expressed as percentages. Understanding percentages allows you to track your progress and predict your final grade.
5. Scientific and Research Applications:
In scientific experiments, percentages are extensively used to represent data, such as the percentage of respondents who agree with a particular opinion in a survey, the percentage change in a population over time, or the percentage of a specific element within a compound.
6. Business and Profit Margins:
Businesses rely heavily on percentage calculations to determine profit margins, markups, discounts, and overall financial performance. Understanding these percentages is crucial for making informed business decisions.
Advanced Percentage Problems: Expanding Your Skills
While the initial problem was straightforward, percentage calculations can become considerably more intricate. Here are some examples of more complex scenarios:
-
Compound Interest: This involves calculating interest not only on the principal amount but also on the accumulated interest from previous periods.
-
Percentage Increase/Decrease: Calculating the percentage change between two values requires understanding the formula [(New Value - Old Value) / Old Value] * 100.
-
Successive Discounts: When applying multiple discounts consecutively, the calculations become more complex as each subsequent discount is applied to the already reduced price.
Mastering Percentages: A Continuous Learning Process
This comprehensive guide has demonstrated different approaches to solving percentage problems, highlighting the practical applications of this crucial mathematical concept. By understanding these methods and practicing regularly, you'll develop a strong foundation in percentage calculations, enabling you to tackle a wide range of challenges in various aspects of your life. Remember, consistent practice is key to mastering any skill, and the world of percentages is no exception. Continue exploring different problems, and you'll find your confidence and proficiency steadily increasing. The journey to mastering percentages is an ongoing process of learning and application, so keep practicing and refining your skills!
Latest Posts
Related Post
Thank you for visiting our website which covers about 50 Is 80 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.