51 Is 85 Of What Number
News Co
Mar 22, 2025 · 5 min read
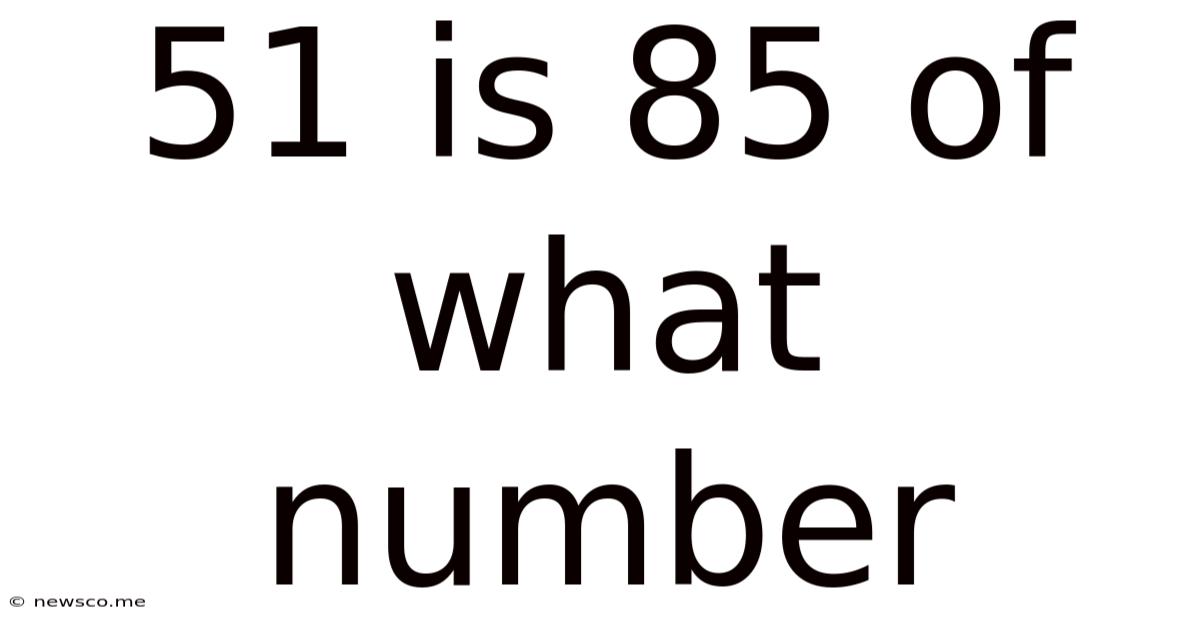
Table of Contents
51 is 85% of What Number? A Comprehensive Guide to Solving Percentage Problems
This seemingly simple question, "51 is 85% of what number?", opens the door to understanding a fundamental concept in mathematics: percentages. While the answer itself is straightforward, the underlying principles and their applications are far-reaching, extending into various fields like finance, statistics, and everyday life. This article will not only solve the problem but also delve into the various methods for solving percentage problems, exploring different approaches and providing practical examples.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction or a ratio expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 85% means 85 out of 100, which can also be written as the fraction 85/100 or the decimal 0.85.
Method 1: Using the Formula
The most common method to solve percentage problems is using the formula:
(Percentage/100) * Whole = Part
In our problem:
- Part: 51 (This is the value representing the percentage)
- Percentage: 85 (This is the percentage value)
- Whole: This is the unknown value we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
(85/100) * x = 51
Now, we solve for 'x':
- Multiply both sides by 100: 85x = 5100
- Divide both sides by 85: x = 5100 / 85
- Calculate: x = 60
Therefore, 51 is 85% of 60.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
51/x = 85/100
This proportion reads: "51 is to x as 85 is to 100." To solve for x, we can cross-multiply:
51 * 100 = 85 * x
5100 = 85x
x = 5100 / 85
x = 60
Again, we find that 51 is 85% of 60.
Method 3: Using Decimal Conversion
Percentages can easily be converted to decimals. To convert a percentage to a decimal, simply divide the percentage by 100. In this case, 85% becomes 0.85. The problem then becomes:
0.85 * x = 51
Solving for x:
x = 51 / 0.85
x = 60
This method yields the same result: 51 is 85% of 60.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world situations. Here are a few examples:
1. Finance:
- Calculating interest: Banks use percentages to calculate interest on loans and savings accounts. Understanding percentage calculations allows you to determine the total amount you'll pay back on a loan or the interest earned on your savings.
- Discounts and sales tax: Sales often involve percentage discounts. Knowing how to calculate percentages helps determine the final price after a discount is applied. Similarly, sales tax is usually calculated as a percentage of the purchase price.
- Investment returns: Investors track their returns on investments using percentages. Understanding percentage changes helps assess the performance of different investments.
2. Statistics:
- Analyzing data: Percentages are frequently used in statistics to represent proportions and probabilities. For example, a survey might show that 70% of respondents prefer a certain product.
- Calculating percentages of a population: Researchers use percentages to represent segments of a population in studies. For example, determining the percentage of a population with a particular characteristic.
3. Everyday Life:
- Tipping in restaurants: Calculating a tip usually involves finding a percentage of the bill.
- Calculating sale prices: Determining the final price of items on sale after a percentage discount is applied.
- Understanding nutritional information: Food labels often show percentages of daily recommended values for various nutrients.
Beyond the Basics: Advanced Percentage Problems
While the problem "51 is 85% of what number?" is relatively straightforward, percentage problems can become more complex. For instance, you might encounter scenarios involving:
- Percentage increase or decrease: Calculating the percentage change between two values.
- Compound interest: Calculating interest on interest over multiple periods.
- Successive discounts: Determining the final price after multiple percentage discounts are applied.
Mastering the fundamental concepts of percentages, as demonstrated in solving "51 is 85% of what number?", provides a solid foundation for tackling these more advanced problems.
Troubleshooting and Common Mistakes
When solving percentage problems, it's important to be mindful of potential pitfalls:
- Incorrect formula application: Ensure you're using the correct formula and substituting the values accurately.
- Misinterpretation of the problem: Carefully read the problem statement to correctly identify the part, percentage, and whole.
- Calculation errors: Double-check your calculations to avoid simple arithmetic mistakes.
- Unit inconsistency: Ensure all units are consistent (e.g., don't mix percentages with decimals without converting).
Conclusion: The Power of Percentage Understanding
The seemingly simple question, "51 is 85% of what number?" highlights the importance of understanding percentages. This fundamental concept underpins numerous applications in various fields, from finance and statistics to everyday life. By mastering different methods for solving percentage problems, including using the formula, proportions, and decimal conversions, individuals equip themselves with valuable skills applicable across a wide range of scenarios. This understanding not only facilitates problem-solving but also empowers individuals to make informed decisions in various aspects of their lives. Remember to practice regularly and to carefully consider potential pitfalls to ensure accurate and efficient calculations. The journey from understanding the basics of percentage calculation to confidently handling complex problems is a rewarding one, opening doors to a deeper appreciation of mathematical concepts and their practical relevance.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 51 Is 85 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.