53 6 As A Mixed Number
News Co
Apr 27, 2025 · 5 min read
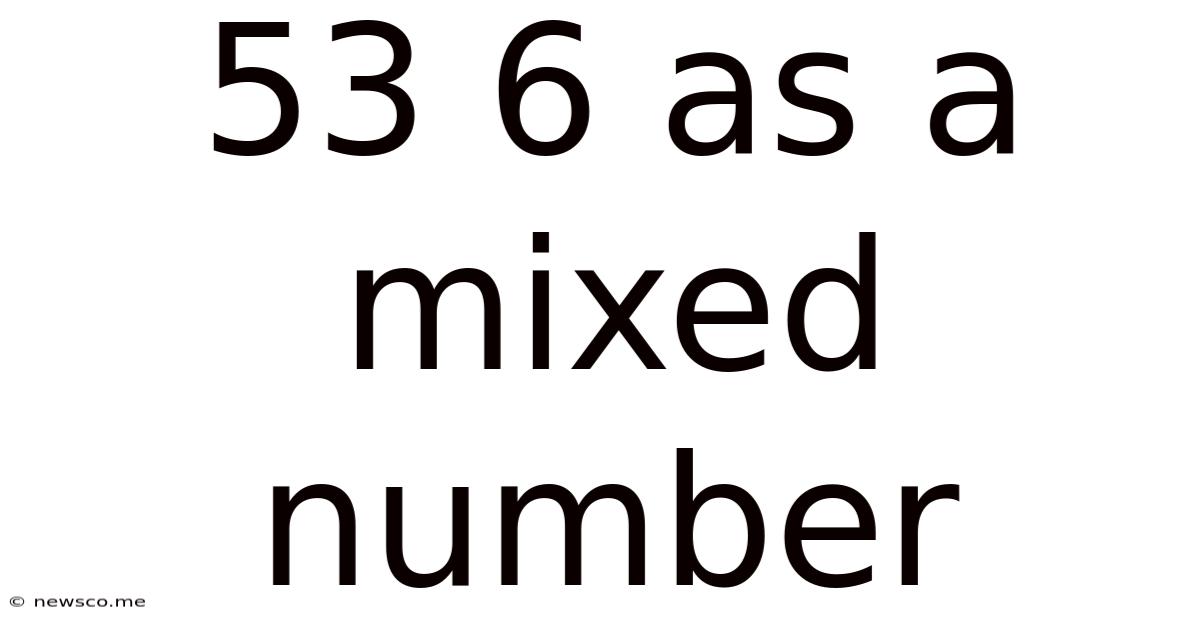
Table of Contents
53/6 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 53/6 into a mixed number, explaining the concept in detail and providing various methods for solving similar problems. We'll also explore the practical applications of mixed numbers and discuss related concepts to solidify your understanding.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number, representing two whole units and three-quarters of another unit. Mixed numbers are incredibly useful in everyday life, from measuring ingredients in cooking to calculating distances.
Converting an Improper Fraction to a Mixed Number
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. The fraction 53/6 is an improper fraction because 53 (the numerator) is larger than 6 (the denominator). To convert an improper fraction to a mixed number, we need to determine how many times the denominator goes into the numerator and what the remainder is.
Step-by-Step Conversion of 53/6
-
Divide the numerator by the denominator: We divide 53 by 6. 53 ÷ 6 = 8 with a remainder of 5.
-
The quotient becomes the whole number: The quotient, 8, becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction: The remainder, 5, becomes the numerator of the fractional part.
-
The denominator remains the same: The denominator remains 6.
Therefore, 53/6 as a mixed number is 8 ⁵⁄₆.
Visualizing the Conversion
Imagine you have 53 identical objects. You want to group them into sets of 6. You can create 8 complete sets of 6, leaving you with 5 objects remaining. This visually represents the conversion: 8 complete sets (the whole number) and 5 objects out of a possible 6 to make another set (the fraction ⁵⁄₆).
Alternative Methods for Conversion
While the long division method is the most common, other methods can help reinforce understanding:
-
Repeated Subtraction: Subtract the denominator (6) repeatedly from the numerator (53) until the result is less than the denominator. Count how many times you subtracted (this is your whole number) and the remaining value is your new numerator.
-
Using Multiplication and Subtraction: Find the largest multiple of the denominator that is less than or equal to the numerator. For 53/6, the largest multiple of 6 less than or equal to 53 is 48 (6 x 8). Subtract 48 from 53 (53 - 48 = 5). The result, 5, becomes the numerator of your fraction, and the multiplier (8) becomes the whole number.
Why Convert to Mixed Numbers?
Mixed numbers offer several advantages over improper fractions:
-
Improved Understanding: Mixed numbers often provide a more intuitive understanding of quantity, especially in real-world applications. It's easier to grasp the concept of "8 and ⁵⁄₆ pizzas" than "53/6 pizzas."
-
Simplified Calculations: In certain calculations, particularly addition and subtraction, working with mixed numbers can be simpler than dealing with large improper fractions.
-
Clearer Communication: Mixed numbers are frequently preferred for communicating quantities in everyday conversations and written explanations.
Working with Mixed Numbers: Addition and Subtraction
Adding and subtracting mixed numbers requires a bit more care than working solely with improper fractions. Here’s a brief overview:
Addition:
- Add the whole numbers: Add the whole number parts of the mixed numbers together.
- Add the fractions: Add the fractional parts. If the resulting fraction is an improper fraction, convert it to a mixed number.
- Combine: Combine the whole number sum and the fractional sum (or the new mixed number from the fractional sum) to get the final answer.
Subtraction:
- Borrowing: If the fraction in the minuend (the number being subtracted from) is smaller than the fraction in the subtrahend (the number being subtracted), you'll need to “borrow” 1 from the whole number part of the minuend. This borrowed 1 is added to the fraction part of the minuend as a fraction with the same denominator.
- Subtract the fractions: Subtract the fractional parts.
- Subtract the whole numbers: Subtract the whole number parts.
- Combine: Combine the whole number difference and the fractional difference for the final answer.
Practical Applications of Mixed Numbers
Mixed numbers are used extensively in various fields:
-
Cooking and Baking: Measuring ingredients accurately often involves mixed numbers (e.g., 2 ½ cups of flour).
-
Construction and Engineering: Precise measurements in construction and engineering projects frequently rely on mixed numbers.
-
Time Measurement: Telling time involves using mixed numbers (e.g., 2:45 or 2 ¾ hours).
-
Data Analysis: Representing data and proportions often involves using mixed numbers for clarity.
Expanding on Fraction Concepts
Understanding 53/6 as a mixed number leads to a broader understanding of fractions:
-
Equivalent Fractions: 53/6 is equivalent to many other fractions (e.g., 106/12, 159/18). These fractions all represent the same quantity.
-
Simplifying Fractions: While 53/6 is an improper fraction, some improper fractions can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In this case, 53/6 is already in its simplest form because 53 is a prime number.
-
Decimal Representation: Improper fractions and mixed numbers can also be expressed as decimals. 53/6 as a decimal is approximately 8.8333...
Conclusion
Converting 53/6 to the mixed number 8 ⁵⁄₆ is a straightforward process with various approaches. Understanding this conversion is crucial for mastering fundamental mathematical concepts and solving real-world problems. By grasping the principles involved, you'll build a strong foundation for more advanced mathematical concepts and confidently apply your knowledge in various situations. Remember that consistent practice is key to mastering fraction manipulation. Continue exploring related concepts, and your confidence in working with fractions will steadily increase.
Latest Posts
Related Post
Thank you for visiting our website which covers about 53 6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.