5x - 15 - 20x 10
News Co
Mar 24, 2025 · 5 min read
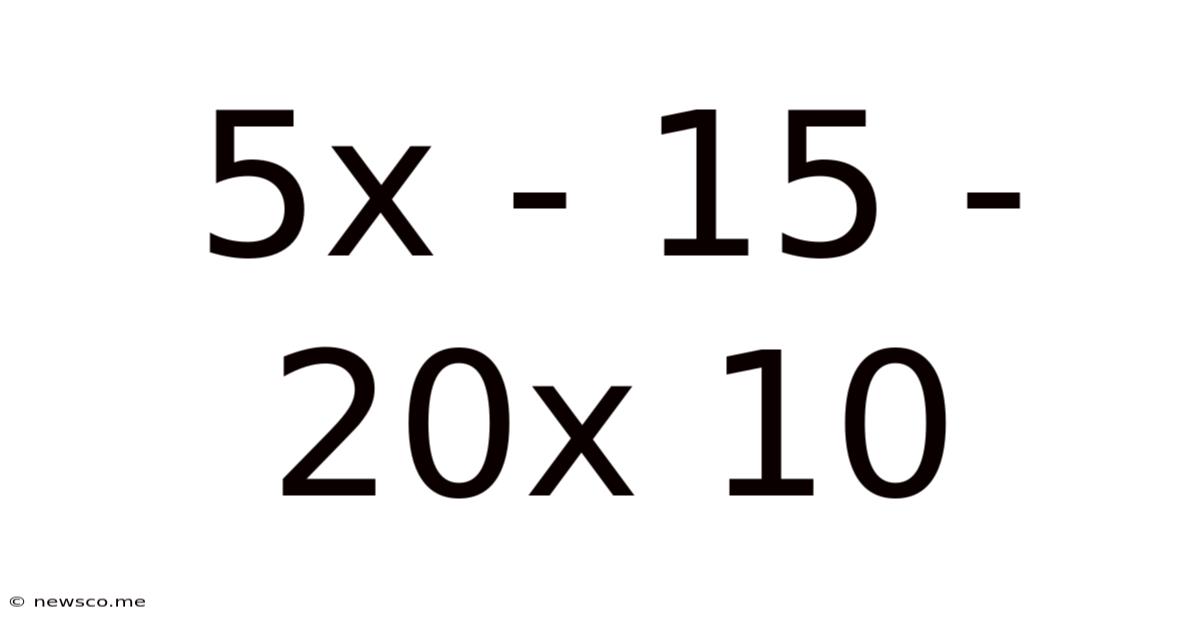
Table of Contents
Decoding the Mathematical Expression: 5x - 15 - 20x + 10
This article delves into the mathematical expression "5x - 15 - 20x + 10," exploring its simplification, applications, and broader mathematical concepts it represents. We'll cover various aspects, from basic algebraic manipulation to potential real-world applications, ensuring a comprehensive understanding for readers of all levels.
Understanding the Components: Variables and Constants
Before tackling the simplification, let's define the elements within the expression:
-
Variables: In mathematics, a variable is a symbol (usually a letter) that represents a quantity that can vary or change. In our expression, 'x' is the variable. It represents an unknown value.
-
Constants: Constants are fixed numerical values that don't change. In our expression, -15 and +10 are constants.
-
Coefficients: A coefficient is a numerical factor that multiplies a variable. In our expression, 5 and -20 are coefficients of the variable 'x'.
-
Operators: Operators are symbols that indicate mathematical operations. In this expression, we have subtraction (-) and addition (+).
Simplifying the Expression: Combining Like Terms
The key to simplifying the expression "5x - 15 - 20x + 10" lies in combining like terms. Like terms are terms that have the same variable raised to the same power. In this case, our like terms are the terms containing 'x' and the constant terms.
Step-by-step simplification:
-
Group like terms: Rearrange the expression to group like terms together: (5x - 20x) + (-15 + 10)
-
Combine the 'x' terms: 5x - 20x = -15x. Remember that subtracting a larger value from a smaller value results in a negative value.
-
Combine the constant terms: -15 + 10 = -5
-
Write the simplified expression: The simplified expression is -15x - 5.
Visualizing the Expression: Graphical Representation
The simplified expression, -15x - 5, represents a linear equation. Linear equations, when graphed, produce straight lines. This allows for a visual representation of the relationship between 'x' and the expression's value.
-
Slope: The coefficient of 'x' (-15) represents the slope of the line. A negative slope indicates that the line decreases as 'x' increases. The steepness of the slope reflects the rate of decrease. In this case, the slope is very steep, indicating a rapid decrease.
-
Y-intercept: The constant term (-5) represents the y-intercept – the point where the line intersects the y-axis (where x = 0).
By plotting these points on a graph and drawing a straight line through them, we can visually represent the expression. This provides a clear understanding of how the value of the expression changes as 'x' varies. Tools like graphing calculators or online graphing utilities can easily generate this graph.
Applications and Real-World Scenarios
While this expression might seem purely abstract, it can represent real-world scenarios. Let’s consider a few examples:
-
Profit/Loss Calculation: Imagine a small business selling handmade items. Let's say 'x' represents the number of items sold. If each item generates a profit of $5, but there are fixed costs of $15 (like rent and materials) and variable costs of $20 per item (like raw materials fluctuating with production), the expression would model their profit: 5x - 15 - 20x + 10. The simplified version, -15x - 5, shows that they are losing $15 per item sold plus an additional $5 in fixed costs. This highlights the need to adjust pricing or reduce costs.
-
Temperature Changes: The expression could model temperature changes over time. 'x' could represent the number of hours, with 5 representing an initial temperature increase, -15 representing a subsequent drop, -20x representing a constant temperature decrease over time, and +10 representing a final temperature adjustment. The simplified expression would then represent the final temperature after 'x' hours.
-
Physics and Motion: In physics, linear equations frequently describe motion. The expression could represent displacement or velocity, with 'x' representing time, and the coefficients representing acceleration, initial velocity, and displacement.
Solving for x: Finding the Roots
While the expression itself doesn't equal anything (it's not an equation), we can explore what values of 'x' would make the expression equal to zero. This involves setting the simplified expression equal to zero and solving for 'x':
-15x - 5 = 0
This is a simple linear equation that can be solved using basic algebra:
-
Add 5 to both sides: -15x = 5
-
Divide both sides by -15: x = -5/15 = -1/3
Therefore, the expression equals zero when x = -1/3. This point represents the x-intercept on the graph.
Expanding on the Concept: Quadratic and Higher-Order Equations
While this specific expression is linear, it’s important to note that more complex expressions can involve higher powers of x, leading to quadratic or even higher-order equations. These equations are significantly more challenging to solve and may have multiple solutions. Understanding the basics of linear equations, as demonstrated here, forms the foundation for tackling more complex mathematical problems.
Practical Exercises for Understanding
To solidify your understanding, consider these exercises:
-
Substitute values: Substitute different values of 'x' (e.g., 0, 1, -1, 2, -2) into both the original and simplified expressions. Verify that both produce the same result. This helps to build confidence in the simplification process.
-
Create your own scenario: Develop a real-world scenario that could be modeled by a linear expression similar to the one we discussed. Write down the expression, simplify it, and interpret the results.
-
Graph the equation: Use a graphing calculator or online tool to graph the equation y = -15x - 5. Observe the slope and y-intercept.
Conclusion: Mastering the Fundamentals of Algebra
The seemingly simple expression "5x - 15 - 20x + 10" provides a gateway to understanding fundamental algebraic concepts like variables, constants, combining like terms, and solving linear equations. By mastering these concepts, you build a strong foundation for tackling more complex mathematical challenges and applying these principles to various real-world scenarios. The ability to simplify expressions and visualize them graphically are crucial skills for success in mathematics and related fields. Remember that consistent practice and a methodical approach are essential for mastering these concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5x - 15 - 20x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.