5x 2y 10 In Slope Intercept Form
News Co
Apr 24, 2025 · 5 min read
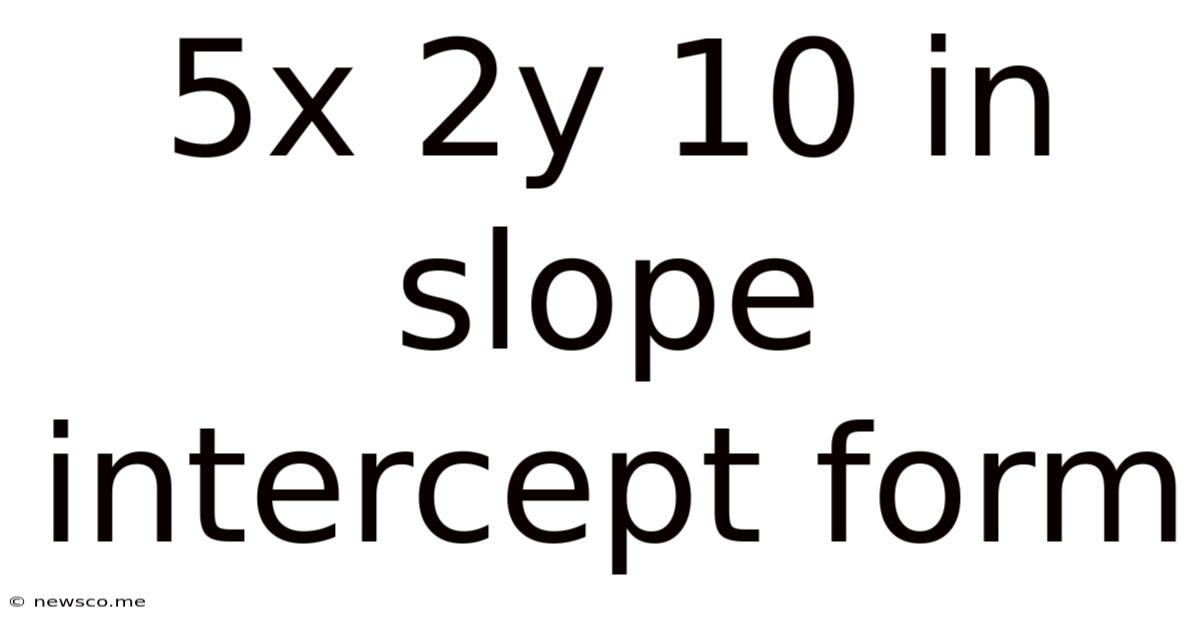
Table of Contents
5x + 2y = 10 in Slope-Intercept Form: A Comprehensive Guide
The equation 5x + 2y = 10 represents a linear relationship between two variables, x and y. While presented in standard form (Ax + By = C), it's often more useful to express this relationship in slope-intercept form (y = mx + b), where 'm' represents the slope and 'b' represents the y-intercept. This guide will walk you through the process of converting 5x + 2y = 10 into slope-intercept form, exploring the significance of the slope and y-intercept, and examining various applications and related concepts.
Understanding Slope-Intercept Form (y = mx + b)
Before diving into the conversion, let's solidify our understanding of the slope-intercept form: y = mx + b.
- y: Represents the dependent variable. Its value depends on the value of x.
- x: Represents the independent variable. Its value is chosen freely.
- m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope means the line rises from left to right, while a negative slope means it falls from left to right. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept. This is the point where the line intersects the y-axis (where x = 0).
Converting 5x + 2y = 10 to Slope-Intercept Form
The conversion process involves isolating 'y' on one side of the equation. Let's break it down step-by-step:
-
Subtract 5x from both sides: This moves the 'x' term to the right side of the equation.
5x + 2y - 5x = 10 - 5x 2y = 10 - 5x -
Divide both sides by 2: This isolates 'y' and gives us the slope-intercept form.
2y / 2 = (10 - 5x) / 2 y = 5 - (5/2)x -
Rearrange for standard form: It's often preferable to present the equation with the 'x' term first.
y = -(5/2)x + 5
Therefore, the slope-intercept form of the equation 5x + 2y = 10 is y = -(5/2)x + 5.
Interpreting the Slope and Y-Intercept
Now that we have the equation in slope-intercept form, we can easily identify the slope and y-intercept:
-
Slope (m) = -5/2: This indicates a negative slope. The line will fall from left to right. The slope tells us that for every 2-unit increase in x, y decreases by 5 units.
-
Y-intercept (b) = 5: This means the line crosses the y-axis at the point (0, 5).
Graphing the Equation
With the slope and y-intercept, graphing the equation becomes straightforward:
-
Plot the y-intercept: Mark the point (0, 5) on the y-axis.
-
Use the slope to find another point: The slope is -5/2. This means from the y-intercept (0, 5), move 2 units to the right and 5 units down. This gives you the point (2, 0).
-
Draw a line: Draw a straight line through the two points (0, 5) and (2, 0). This line represents the equation 5x + 2y = 10.
Applications and Related Concepts
The equation 5x + 2y = 10, and its slope-intercept equivalent, has various applications across different fields:
1. Linear Programming
In linear programming, this equation could represent a constraint in an optimization problem. For example, it might define a budget constraint where 5x represents the cost of one item and 2y represents the cost of another, with a total budget of 10 units.
2. Economics
This equation could model a simple supply and demand scenario, where x and y represent quantities of a good and their respective prices. The slope would represent the responsiveness of demand to price changes.
3. Physics
In physics, it might represent a relationship between velocity and time, or distance and time, depending on the context.
4. Computer Graphics
In computer graphics, linear equations are fundamental to defining lines and shapes. The equation helps in generating points to draw a line on a screen.
Finding the x-intercept
While the y-intercept is readily available from the slope-intercept form, the x-intercept (where y = 0) can be found by substituting y = 0 into the original equation or the slope-intercept form:
Using the original equation:
5x + 2(0) = 10 5x = 10 x = 2
The x-intercept is (2, 0).
Using the slope-intercept form:
0 = -(5/2)x + 5 (5/2)x = 5 x = 2
This confirms the x-intercept is (2, 0).
Parallel and Perpendicular Lines
Understanding the slope allows us to determine equations of lines that are parallel or perpendicular to the line represented by 5x + 2y = 10.
-
Parallel Lines: Parallel lines have the same slope. Any line with a slope of -5/2 will be parallel to the line represented by our equation.
-
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. The negative reciprocal of -5/2 is 2/5. Any line with a slope of 2/5 will be perpendicular to the line represented by our equation.
Solving Systems of Equations
The equation 5x + 2y = 10 can be part of a system of linear equations. Solving a system of equations involves finding the values of x and y that satisfy all equations simultaneously. Methods like substitution or elimination can be used to solve these systems.
Conclusion
Converting the equation 5x + 2y = 10 into slope-intercept form, y = -(5/2)x + 5, provides a valuable and readily interpretable representation of the linear relationship between x and y. Understanding the slope and y-intercept allows for easy graphing, identification of parallel and perpendicular lines, and application in various contexts, from linear programming to physics and computer graphics. The process of conversion itself reinforces fundamental algebraic manipulations, demonstrating the interconnectedness of different forms of linear equations. Mastering this conversion and understanding its implications is crucial for anyone working with linear relationships in mathematics and related fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5x 2y 10 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.