6/8 Is Equal To What Fraction
News Co
Mar 30, 2025 · 5 min read
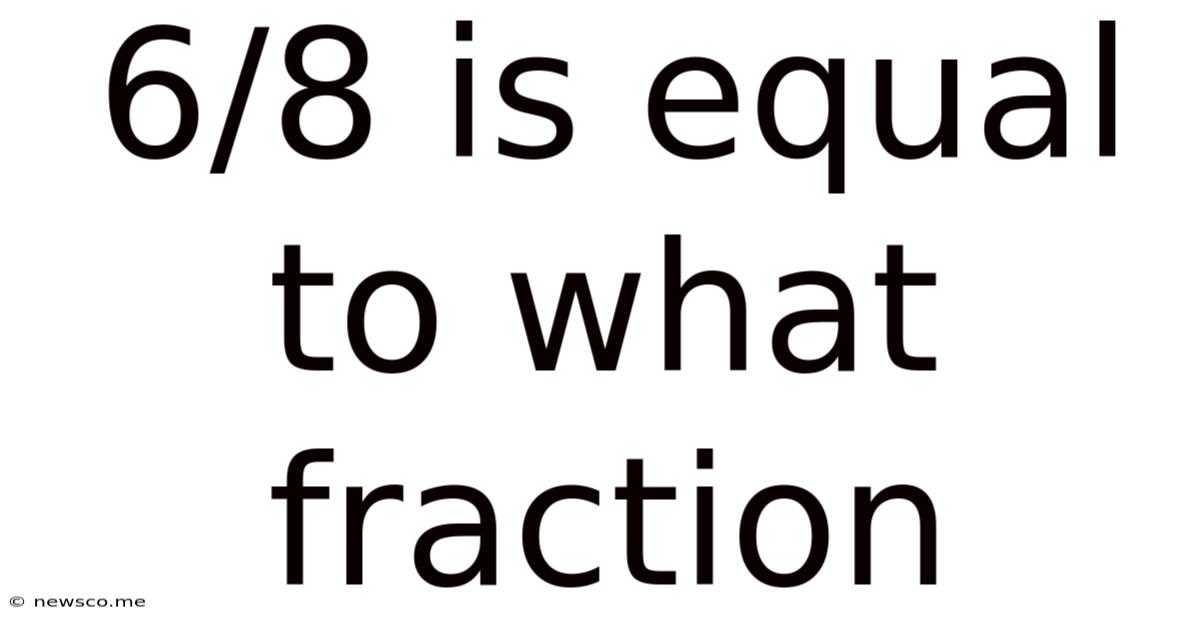
Table of Contents
6/8 is Equal to What Fraction? A Deep Dive into Fraction Simplification
The question, "6/8 is equal to what fraction?" might seem simple at first glance, but it opens the door to a deeper understanding of fractions, simplification, and equivalent fractions. This comprehensive guide will not only answer the question directly but also explore the underlying mathematical principles and provide you with the tools to simplify any fraction with confidence.
Understanding Fractions
Before we tackle 6/8, let's establish a firm grasp of what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 6/8, 6 is the numerator and 8 is the denominator. This means we have 6 parts out of a possible 8 equal parts.
Simplifying Fractions: The Concept of Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its simplest form. This involves finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Finding the GCD can be done in several ways:
-
Listing Factors: List all the factors of both the numerator and the denominator. The largest factor common to both is the GCD.
-
Prime Factorization: Break down both the numerator and the denominator into their prime factors (numbers only divisible by 1 and themselves). The GCD is the product of the common prime factors raised to the lowest power.
-
Euclidean Algorithm: This is a more efficient method for larger numbers, involving a series of divisions until the remainder is 0. The last non-zero remainder is the GCD.
Simplifying 6/8
Let's apply these methods to simplify 6/8:
Method 1: Listing Factors
Factors of 6: 1, 2, 3, 6 Factors of 8: 1, 2, 4, 8
The largest common factor is 2.
Method 2: Prime Factorization
6 = 2 x 3 8 = 2 x 2 x 2 = 2³
The common prime factor is 2 (to the power of 1, as that's the lowest power present in both).
Method 3: Euclidean Algorithm
8 ÷ 6 = 1 with a remainder of 2 6 ÷ 2 = 3 with a remainder of 0
The last non-zero remainder is 2.
In all three methods, we find the GCD of 6 and 8 is 2. Now, we divide both the numerator and the denominator by 2:
6 ÷ 2 = 3 8 ÷ 2 = 4
Therefore, 6/8 simplifies to 3/4.
Visualizing the Simplification
Imagine a pizza cut into 8 equal slices. You have 6 slices (6/8). If you group the slices into pairs (2 slices per group), you have 3 pairs out of a possible 4 pairs (3/4). This visual representation reinforces the equivalence of 6/8 and 3/4.
Equivalent Fractions
It's crucial to understand that 6/8 and 3/4 are equivalent fractions. Equivalent fractions represent the same portion of a whole, even though they look different. You can obtain equivalent fractions by multiplying or dividing both the numerator and denominator by the same non-zero number.
For example:
- Multiplying 3/4 by 2/2 (which equals 1, so it doesn't change the value): (3 x 2) / (4 x 2) = 6/8
- Dividing 6/8 by 2/2: (6 ÷ 2) / (8 ÷ 2) = 3/4
This illustrates the reversible nature of simplification: you can simplify a fraction to its lowest terms and then build equivalent fractions by multiplying.
Applications of Fraction Simplification
The ability to simplify fractions is fundamental in various areas:
-
Mathematics: Simplifying fractions makes calculations easier and more manageable. It's essential for adding, subtracting, multiplying, and dividing fractions.
-
Science: Many scientific measurements and calculations involve fractions. Simplifying fractions ensures accuracy and clarity in scientific reporting.
-
Engineering: Engineers use fractions extensively in design and construction. Simplified fractions improve the precision and efficiency of engineering work.
-
Cooking and Baking: Recipes often use fractions to specify ingredient amounts. Simplifying fractions helps in accurately measuring ingredients.
-
Everyday Life: We encounter fractions in various daily situations, from sharing items equally to calculating discounts. Understanding fraction simplification makes these tasks easier.
Beyond 6/8: Simplifying Other Fractions
The process of simplifying fractions remains the same regardless of the numbers involved. Always look for the greatest common divisor and divide both the numerator and the denominator by it.
Let's consider another example: 12/18
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 18: 1, 2, 3, 6, 9, 18
The GCD is 6.
12 ÷ 6 = 2 18 ÷ 6 = 3
Therefore, 12/18 simplifies to 2/3.
Mastering Fraction Simplification: Tips and Tricks
-
Practice regularly: The more you practice, the faster and more confident you'll become.
-
Use different methods: Try all three GCD methods (listing factors, prime factorization, Euclidean algorithm) to find the most efficient approach for different numbers.
-
Start with small fractions: Begin with simple fractions and gradually increase the complexity.
-
Check your work: Always double-check your simplified fraction to ensure it's in its lowest terms.
-
Utilize online resources: Many websites and apps offer fraction simplification tools and practice exercises. These can be helpful supplementary learning tools.
Conclusion: The Importance of Understanding Fractions
The seemingly straightforward question of simplifying 6/8 reveals the underlying power and significance of understanding fractions and their simplification. This process isn't just about reducing numbers; it's about mastering a fundamental mathematical concept that has broad applications in various fields and daily life. By understanding and applying the principles outlined in this guide, you can confidently tackle any fraction simplification problem and build a solid foundation in mathematics. Remember to practice regularly to hone your skills and build confidence in your ability to work with fractions.
Latest Posts
Related Post
Thank you for visiting our website which covers about 6/8 Is Equal To What Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.