60 Is 12 Percent Of What Number
News Co
Apr 15, 2025 · 4 min read
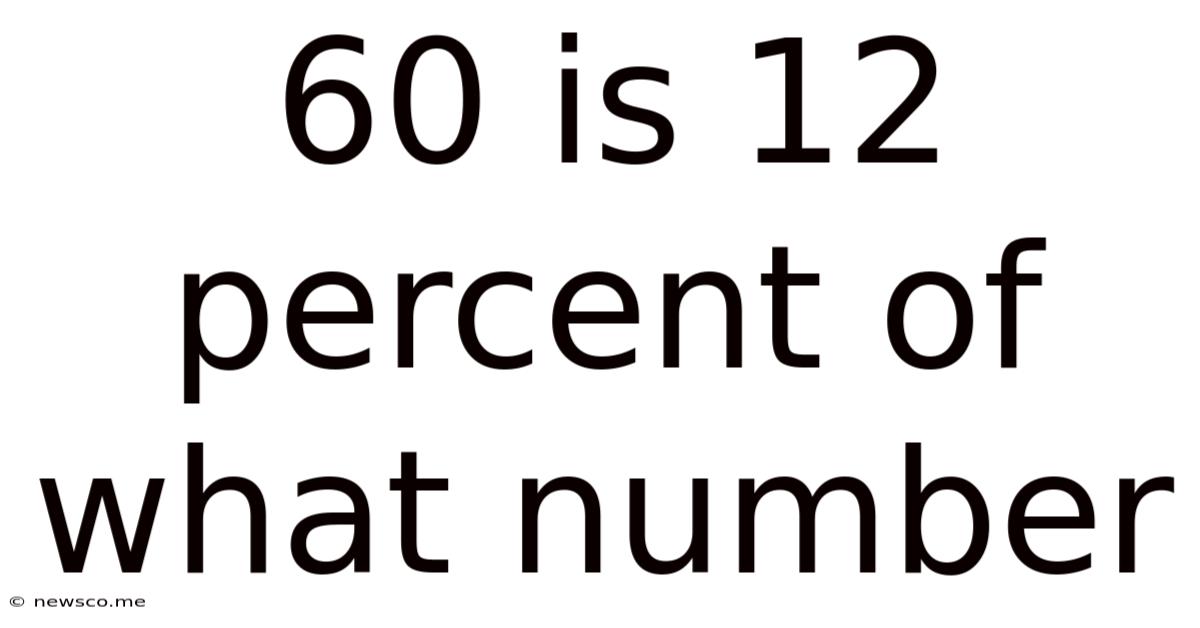
Table of Contents
60 is 12 Percent of What Number: A Comprehensive Guide to Percentage Calculations
This article delves into the question: "60 is 12 percent of what number?" We'll not only solve this specific problem but also explore the broader concept of percentage calculations, providing you with the tools and understanding to tackle similar problems with ease. We'll cover various methods, from basic algebra to using proportions and even explore practical applications of percentage calculations in everyday life.
Understanding Percentages:
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using Algebra
This is perhaps the most straightforward and commonly used method to solve percentage problems. We can translate the problem "60 is 12 percent of what number" into an algebraic equation:
- Let 'x' represent the unknown number.
- 12% can be written as 0.12 (12/100).
- The equation becomes: 60 = 0.12x
To solve for 'x', we simply divide both sides of the equation by 0.12:
x = 60 / 0.12 x = 500
Therefore, 60 is 12 percent of 500.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion where one ratio represents the known percentage and the other represents the unknown number.
- We know that 60 is 12% of the unknown number (x). This can be written as a ratio: 60/x
- We also know that 12% can be written as 12/100.
- Therefore, we can set up the following proportion:
60/x = 12/100
To solve for 'x', we cross-multiply:
60 * 100 = 12 * x 6000 = 12x x = 6000 / 12 x = 500
Again, we find that 60 is 12 percent of 500.
Method 3: Working Backwards from the Percentage
This method involves understanding the relationship between the percentage and the whole. If 12% is equal to 60, we can find the value of 1% by dividing 60 by 12:
60 / 12 = 5
This means 1% of the unknown number is 5. To find the whole number (100%), we multiply 5 by 100:
5 * 100 = 500
This confirms once more that 60 is 12 percent of 500.
Practical Applications of Percentage Calculations:
Percentage calculations are ubiquitous in everyday life. Understanding them is crucial for navigating various situations, including:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentages. For example, understanding percentage increases and decreases is essential for tracking the performance of investments or understanding the impact of inflation.
-
Shopping: Sales and discounts are often expressed as percentages. Being able to quickly calculate the final price after a discount can save you money and make you a savvy shopper.
-
Science: Percentages are fundamental in scientific calculations and data analysis, allowing scientists to express quantities relative to a whole. This is crucial for fields like chemistry, biology, and statistics.
-
Data Analysis: Understanding percentages is crucial for interpreting data. For example, in surveys, results are often expressed as percentages to indicate the proportion of respondents who chose a particular option. This enables easier comparison and clearer communication of findings.
-
Real Estate: When buying or selling a property, you need to understand how property taxes, commissions, and other fees are calculated, all of which involve percentages. Knowing these will empower you to make informed financial decisions.
Troubleshooting Common Percentage Calculation Errors:
Even with a good grasp of the concepts, errors can creep into calculations. Here are some common mistakes to watch out for:
-
Incorrect Conversion of Percentages to Decimals: Remember to convert percentages to decimals (divide by 100) before using them in calculations. Using 12% instead of 0.12 will lead to an incorrect answer.
-
Misinterpreting the Problem: Always carefully read the word problem to ensure you understand what is being asked. Identify the known values and the unknown value you need to calculate.
-
Calculation Errors: Always double-check your calculations, especially when working with decimals or fractions. Use a calculator if needed to minimize the chance of errors.
-
Rounding Errors: Be mindful of rounding numbers. Excessive rounding during intermediate calculations can lead to inaccuracies in the final answer.
Expanding Your Percentage Skills:
To further solidify your understanding of percentages, consider exploring these related concepts:
-
Percentage Change: This involves calculating the increase or decrease in a value as a percentage of the original value.
-
Percentage Increase/Decrease: Understanding how to calculate percentage increases and decreases is crucial for a wide range of applications including financial analysis, population growth, and economic indicators.
-
Compound Interest: This involves calculating interest on the principal amount plus accumulated interest from previous periods.
By mastering percentage calculations, you equip yourself with a powerful tool applicable across various aspects of life. The ability to perform these calculations efficiently and accurately is valuable in academic pursuits, professional settings, and everyday decision-making. Practice is key – the more you work with percentages, the more comfortable and confident you’ll become. Remember to break down complex problems into smaller, manageable steps, and always double-check your work to ensure accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Is 12 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.