60 Is 15 Of What Number
News Co
Mar 31, 2025 · 4 min read
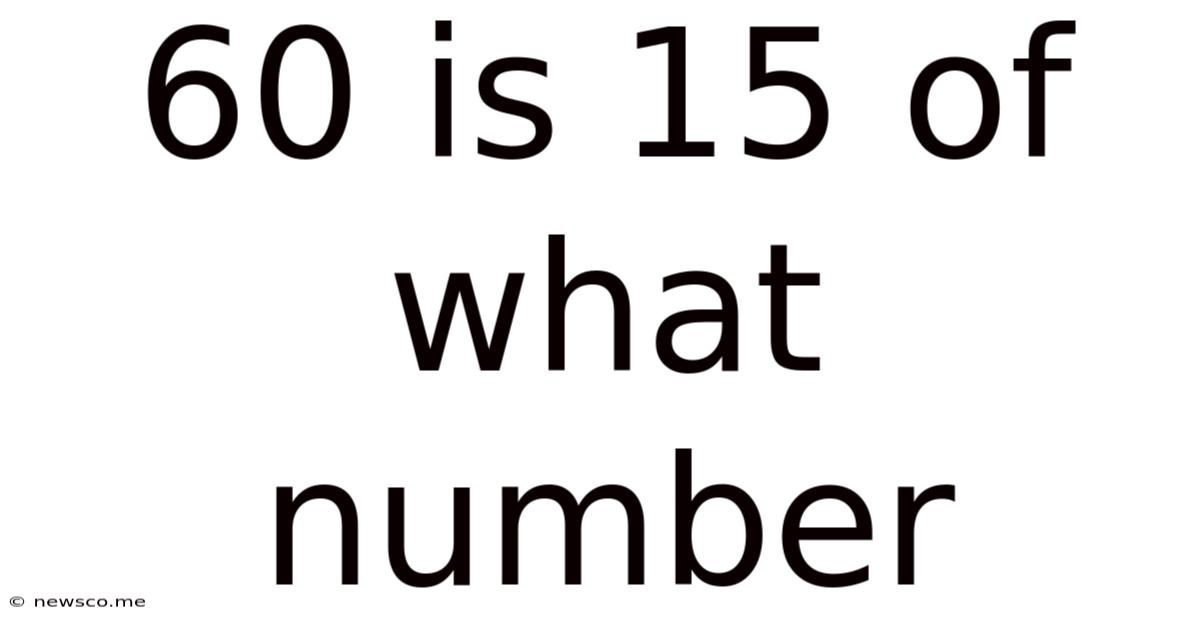
Table of Contents
60 is 15% of What Number? Understanding Percentages and Their Applications
Finding the whole number when you know a percentage and its corresponding part is a fundamental concept in mathematics with widespread applications across various fields. This article delves deep into solving the problem "60 is 15% of what number?", exploring different approaches to arrive at the solution, understanding the underlying mathematical principles, and demonstrating its relevance in real-world scenarios. We'll cover everything from basic percentage calculations to advanced applications and troubleshooting common errors.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." For example, 15% means 15 out of 100, which can be written as the fraction 15/100 or the decimal 0.15. Understanding this fundamental concept is crucial to solving percentage problems.
Method 1: Using the Percentage Formula
The most straightforward method to solve "60 is 15% of what number?" involves using the standard percentage formula:
Part = Percentage × Whole
In our problem:
- Part: 60 (This is the given part of the whole)
- Percentage: 15% (or 0.15 as a decimal)
- Whole: This is what we need to find (let's represent it as 'x')
Substituting these values into the formula, we get:
60 = 0.15 × x
To solve for x, we divide both sides of the equation by 0.15:
x = 60 / 0.15
x = 400
Therefore, 60 is 15% of 400.
Method 2: Using Proportions
Another effective method is setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up a proportion as follows:
15/100 = 60/x
This proportion reads: "15 is to 100 as 60 is to x." To solve for x, we can cross-multiply:
15x = 6000
Now, divide both sides by 15:
x = 6000 / 15
x = 400
Again, we find that 60 is 15% of 400.
Method 3: Working with Decimals
This method is essentially a variation of Method 1 but emphasizes working directly with decimal equivalents. We know that 15% is equal to 0.15. The problem can be rewritten as:
60 = 0.15 * x
Dividing both sides by 0.15:
x = 60 / 0.15 = 400
This confirms our previous results.
Real-World Applications
The ability to solve percentage problems like "60 is 15% of what number?" is incredibly useful in many real-world situations:
-
Business and Finance: Calculating profit margins, discounts, sales tax, interest rates, and investment returns all rely on understanding percentages. For instance, if a business made a profit of $60,000, representing 15% of its total revenue, finding the total revenue would involve this same type of calculation.
-
Science and Engineering: Percentages are used extensively in scientific data analysis, expressing experimental error, statistical significance, and various measurements.
-
Everyday Life: Calculating tips in restaurants, understanding discounts at stores, and comprehending loan interest rates are everyday applications of percentage calculations.
-
Data Analysis: In data analysis, percentages are crucial for summarizing and interpreting data, such as understanding market share or demographic breakdowns.
Troubleshooting Common Errors
When working with percentages, several common errors can occur:
-
Incorrect Conversion to Decimal: A frequent mistake is incorrectly converting a percentage to a decimal. Remember to divide the percentage by 100 (or move the decimal point two places to the left). For example, 15% is 0.15, not 1.5.
-
Incorrect Formula Application: Ensure you are using the correct formula and substituting the values in the right places. Double-check your work to avoid calculation errors.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple steps in the calculation. Round off only at the final stage of the calculation to maintain accuracy.
-
Mixing Up Part and Whole: Clearly identify the "part" and the "whole" in the problem to avoid confusion.
Advanced Applications and Extensions
The fundamental concept of finding the whole from a part and its percentage can be extended to more complex scenarios:
-
Multiple Percentages: Imagine a scenario where a product is initially discounted by 20%, and then a further 10% discount is applied. Understanding percentage calculations is crucial to determining the final price.
-
Compound Interest: Calculating compound interest involves repeatedly applying a percentage increase over time.
-
Tax Calculations: Calculating various types of taxes, like sales tax or income tax, involves intricate percentage calculations.
-
Statistical Analysis: Confidence intervals and hypothesis testing in statistics frequently involve percentage calculations.
Conclusion
Solving the problem "60 is 15% of what number?" is not just an isolated mathematical exercise; it's a gateway to understanding a crucial concept with vast practical implications. Mastering percentage calculations, through various approaches like using the percentage formula, proportions, or decimal manipulation, equips you with a powerful tool applicable across numerous disciplines and everyday life situations. By understanding the underlying principles and avoiding common errors, you can confidently tackle percentage problems of increasing complexity and apply this knowledge effectively in various real-world contexts. Remember to practice regularly to solidify your understanding and improve your speed and accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Is 15 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.