60 Is 20 Of What Number
News Co
May 08, 2025 · 4 min read
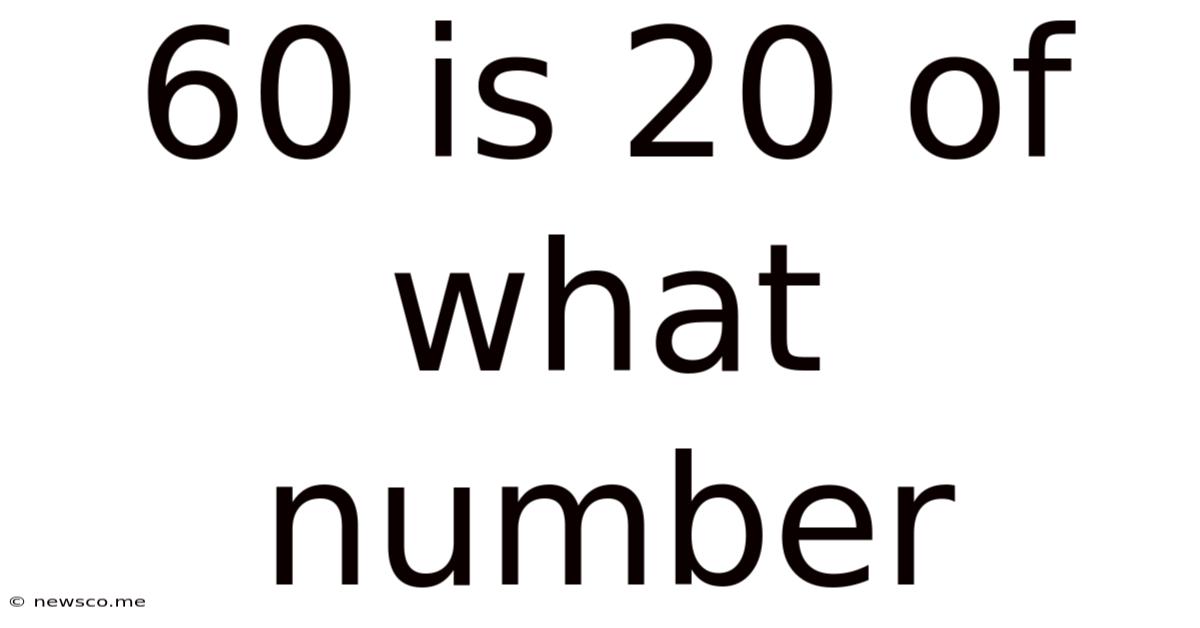
Table of Contents
60 is 20% of What Number? A Deep Dive into Percentage Calculations
This seemingly simple question, "60 is 20% of what number?", opens the door to a fascinating exploration of percentages, their applications, and the underlying mathematical principles. While the answer itself is readily obtainable, understanding the how and why behind the calculation is crucial for anyone looking to master percentage problems and apply this knowledge in various contexts. This comprehensive guide will not only provide the solution but also delve into the different methods for solving percentage problems, exploring their practical uses and tackling more complex scenarios.
Understanding Percentages: The Foundation
Percentages are simply fractions expressed as parts of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of one hundred." Therefore, 20% signifies 20 parts out of a total of 100 parts. This fundamental understanding forms the bedrock of all percentage calculations.
Key Terms and Concepts
Before we dive into the solution, let's clarify some key terms:
- Percentage: The portion of a whole expressed as a number out of 100. Represented by the symbol %.
- Part: The specific amount representing a percentage of the whole. In our question, 60 is the part.
- Whole: The total amount from which the percentage is derived. This is the unknown we need to find.
- Rate: The percentage itself, expressed as a decimal or fraction. In our case, the rate is 20%.
Method 1: Using the Percentage Formula
The most straightforward method to solve "60 is 20% of what number?" involves applying the standard percentage formula:
Part = Rate × Whole
In our problem:
- Part = 60
- Rate = 20% = 0.20 (Converting the percentage to a decimal by dividing by 100)
- Whole = x (This is the unknown we're solving for)
Substituting these values into the formula, we get:
60 = 0.20 × x
To solve for x, we divide both sides of the equation by 0.20:
x = 60 / 0.20
x = 300
Therefore, 60 is 20% of 300.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. Proportions equate two ratios, allowing us to solve for the unknown value. We can represent the problem as:
60/x = 20/100
This proportion states that the ratio of the part (60) to the whole (x) is equal to the ratio of the percentage (20) to 100.
To solve this proportion, we can cross-multiply:
60 × 100 = 20 × x
6000 = 20x
Now, divide both sides by 20:
x = 6000 / 20
x = 300
Again, we find that 60 is 20% of 300.
Method 3: Using the "Is/Of" Method
This simplified method is particularly helpful for beginners. It directly translates the words of the problem into an equation:
"60 is 20% of what number?" becomes:
60 = 0.20 × x
This equation is identical to the one we derived using the percentage formula, leading us to the same solution: x = 300.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, profits, and losses.
- Business: Analyzing sales figures, market share, and profit margins.
- Science: Representing experimental data, statistical analysis, and probability.
- Everyday Life: Calculating tips, understanding sale prices, and determining proportions in recipes.
Tackling More Complex Percentage Problems
The fundamental principles discussed above can be applied to solve more complex problems. Let's consider a few examples:
Example 1: Finding the Percentage Increase or Decrease
Suppose a product's price increased from $100 to $120. What is the percentage increase?
First, find the difference: $120 - $100 = $20
Then, divide the difference by the original price and multiply by 100:
($20 / $100) × 100 = 20%
The price increased by 20%.
Example 2: Calculating the Original Price after a Discount
A shirt is on sale for $40 after a 25% discount. What was the original price?
Let x be the original price. The discount is 25% of x, which is 0.25x. The sale price is the original price minus the discount:
x - 0.25x = $40
0.75x = $40
x = $40 / 0.75
x = $53.33 (approximately)
The original price was approximately $53.33.
Example 3: Solving for Multiple Percentages
If 30% of a number is 60, and 15% of the same number is added, what is the total?
First, find the number:
60 = 0.30x
x = 60 / 0.30 = 200
Then, find 15% of 200:
0.15 × 200 = 30
Finally, add the two values: 60 + 30 = 90
The total is 90.
Conclusion: Mastering Percentage Calculations
The question, "60 is 20% of what number?" serves as a gateway to understanding the broader world of percentage calculations. By mastering the different methods – using the percentage formula, setting up proportions, or employing the "Is/Of" method – you equip yourself with a powerful tool applicable across various disciplines and everyday situations. Remember that consistent practice is key to solidifying your understanding and building confidence in tackling increasingly complex percentage problems. The ability to solve percentage problems efficiently and accurately is an invaluable skill that enhances your problem-solving abilities and opens doors to a deeper understanding of quantitative data.
Latest Posts
Latest Posts
-
8 1 4 As A Fraction
May 09, 2025
-
How To Find A1 In Arithmetic Sequence
May 09, 2025
-
Subtracting A Positive Integer From A Negative Integer
May 09, 2025
-
The Diagonals Of A Parallelogram Are Equal
May 09, 2025
-
Angle Pairs Worksheet Geometry Answer Key
May 09, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.