60 Is 20 Percent Of What Number
News Co
Apr 27, 2025 · 5 min read
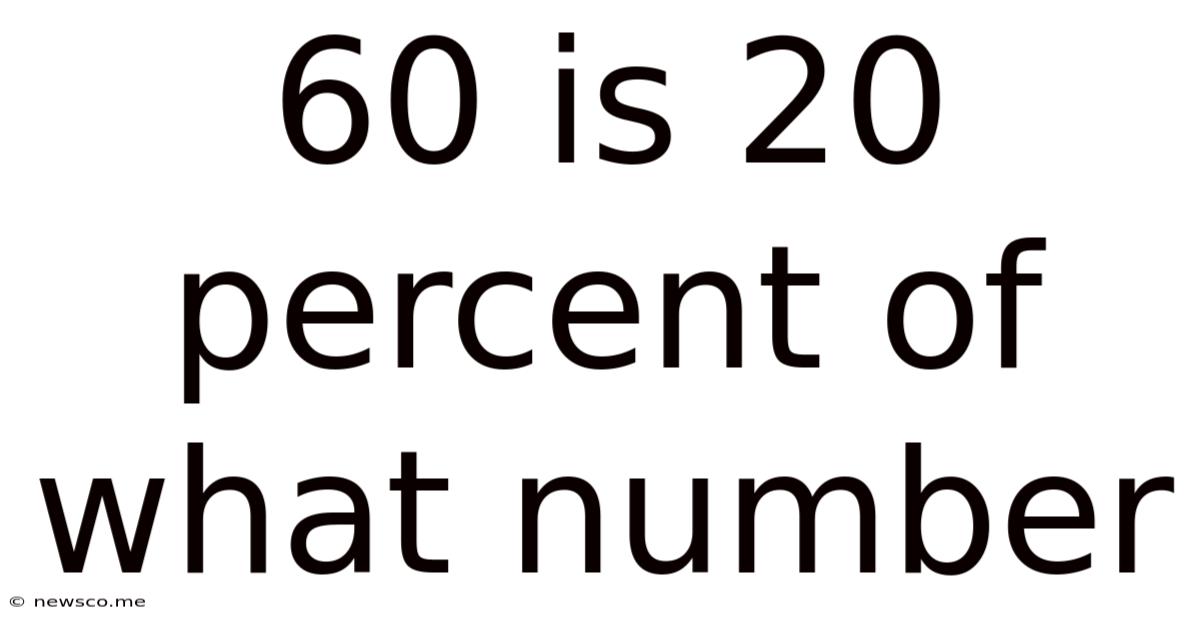
Table of Contents
60 is 20 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Finding a whole number when you know a percentage of it is a common mathematical problem encountered in various fields, from everyday budgeting to complex financial analyses. This comprehensive guide will not only show you how to solve the problem "60 is 20 percent of what number?" but also equip you with the understanding and skills to tackle similar percentage calculations effectively. We'll explore different methods, provide practical examples, and delve into the underlying concepts to solidify your grasp of percentages.
Understanding Percentages
Before diving into the solution, let's briefly review what percentages represent. A percentage is a fraction or ratio expressed as a number out of 100. For instance, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. Percentages are used to represent parts of a whole, making it easier to compare and understand proportions.
Method 1: Using the Equation
The most straightforward way to solve "60 is 20 percent of what number?" is by setting up an equation. We can represent the problem as:
20% * x = 60
Where 'x' represents the unknown number we're trying to find.
To solve for 'x', we first convert the percentage to a decimal by dividing by 100:
20% = 20/100 = 0.2
Now, substitute this into the equation:
0.2 * x = 60
To isolate 'x', divide both sides of the equation by 0.2:
x = 60 / 0.2
x = 300
Therefore, 60 is 20 percent of 300.
Method 2: Using Proportions
Proportions offer another effective approach to solving percentage problems. A proportion is a statement that two ratios are equal. We can set up a proportion based on the given information:
20/100 = 60/x
This proportion states that the ratio of 20 to 100 is equal to the ratio of 60 to the unknown number (x).
To solve for 'x', we cross-multiply:
20 * x = 100 * 60
20x = 6000
Now, divide both sides by 20:
x = 6000 / 20
x = 300
Again, we find that 60 is 20 percent of 300.
Method 3: Using the Percentage Formula
The percentage formula provides a more general approach to various percentage calculations. The formula is:
(Part / Whole) * 100% = Percentage
In our problem, we know the part (60) and the percentage (20%). We need to find the whole. Let's rearrange the formula to solve for the whole:
Whole = Part / (Percentage / 100%)
Substituting the known values:
Whole = 60 / (20 / 100)
Whole = 60 / 0.2
Whole = 300
This method confirms that 60 is 20 percent of 300.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are some examples:
-
Sales and Discounts: If a store offers a 20% discount on an item priced at $60, how much would the item originally cost? This is exactly the same problem we've solved. The original price was $300.
-
Financial Calculations: Calculating interest earned on savings accounts, determining loan payments, and analyzing investment returns often involve percentage calculations. For example, if you earned $60 interest which represents 20% of your total savings, your total savings would be $300.
-
Data Analysis: In statistics and data analysis, percentages are used to represent proportions within datasets. Understanding percentages helps in interpreting and drawing conclusions from data. If a survey showed that 60 out of 300 people preferred a certain product (which is 20%), this helps understand market share and customer preferences.
-
Grade Calculations: Let's say you scored 60 points on a test, and this score represents 20% of your total possible score. What was the total possible score on the test? Applying the same formula, the total possible score was 300 points.
-
Tax Calculations: If you paid $60 in taxes, and this represents 20% of your income, your total income is $300.
Troubleshooting and Common Mistakes
When working with percentages, several common mistakes can occur:
-
Incorrect Decimal Conversion: Failing to correctly convert percentages to decimals (e.g., 20% to 0.2) is a frequent source of error. Always double-check your decimal conversion.
-
Mixing up Part and Whole: Carefully identify the "part" and the "whole" in the problem. The "part" is the portion of the whole that represents the given percentage.
-
Incorrect Formula Application: Ensure you're using the correct formula and applying it correctly. Double-check your calculations to avoid arithmetic errors.
-
Unit Inconsistency: If you're working with mixed units (e.g., dollars and cents, kilograms and grams), make sure to convert them to a consistent unit before proceeding with the calculation.
-
Rounding Errors: When rounding numbers, be aware that this can introduce small errors in the final result. It's advisable to carry out calculations to several decimal places before rounding to the final answer.
Advanced Percentage Calculations
While we've focused on the basic problem, the principles and techniques discussed extend to more complex percentage calculations. This includes:
- Calculating percentage increase or decrease: Determining the percentage change between two values.
- Compound interest calculations: Where interest is calculated on both the principal and accumulated interest.
- Percentage points: Understanding the difference between percentage change and percentage points.
Conclusion
Solving percentage problems, such as "60 is 20 percent of what number?", is a fundamental skill applicable in numerous contexts. This guide has presented various methods – using equations, proportions, and the percentage formula – to solve this type of problem effectively. By understanding the underlying concepts and practicing different approaches, you'll gain confidence and proficiency in handling various percentage calculations with accuracy and efficiency. Remember to always carefully examine the problem, correctly identify the known and unknown variables, and systematically apply the chosen method. With practice and attention to detail, mastering percentage calculations will become second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Is 20 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.