60 Is 25 Of What Number
News Co
Apr 20, 2025 · 4 min read
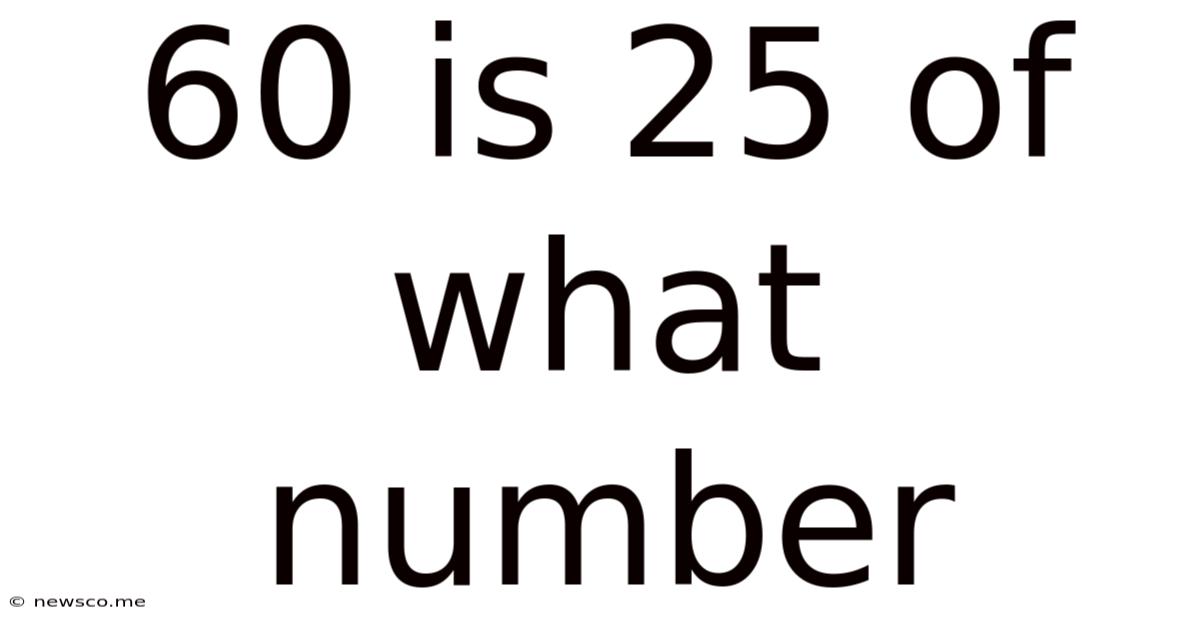
Table of Contents
60 is 25% of What Number? Unraveling Percentages and Proportions
Finding the whole when you know a part and its percentage is a common mathematical problem. This article will delve into the solution for the question: "60 is 25% of what number?" We'll explore various methods to solve this, from basic percentage calculations to using proportions and even algebraic equations. Understanding these techniques will equip you with valuable skills applicable to a wide range of situations, from calculating discounts to determining growth rates.
Understanding Percentages
Before we dive into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For example, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Percentages are used extensively to represent proportions, rates, and changes in various contexts.
Method 1: Using the Percentage Formula
The most straightforward approach to solving "60 is 25% of what number?" is using the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part: 60
- Percentage: 25% = 0.25 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole: This is what we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
60 = 0.25 × x
To solve for x, we divide both sides of the equation by 0.25:
x = 60 / 0.25
x = 240
Therefore, 60 is 25% of 240.
Method 2: Setting up a Proportion
Proportions offer another effective way to solve percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion using the given information:
60/x = 25/100
Here, 60 represents the part, x represents the whole, and 25/100 represents the percentage. To solve for x, we can cross-multiply:
60 × 100 = 25 × x
6000 = 25x
x = 6000 / 25
x = 240
Again, we find that 60 is 25% of 240.
Method 3: Using the Decimal Equivalent
As mentioned earlier, 25% is equivalent to 0.25. We can directly use this decimal equivalent in our calculation:
60 = 0.25 * x
x = 60 / 0.25
x = 240
This method emphasizes the direct relationship between percentages and their decimal forms, providing a concise solution.
Method 4: Algebraic Approach
This method formalizes the problem into an algebraic equation:
Let x represent the unknown number. The problem translates to:
0.25x = 60
Solving for x:
x = 60 / 0.25
x = 240
This approach clearly demonstrates the underlying algebraic structure of the percentage problem.
Real-World Applications
Understanding how to calculate percentages and proportions is crucial in many everyday situations:
1. Sales and Discounts:
Imagine a store offers a 25% discount on an item originally priced at $240. Using our knowledge, we can easily calculate the discount amount: 25% of $240 is $60. The sale price would then be $240 - $60 = $180.
2. Tax Calculations:
If a sales tax is 6%, and you purchase an item for $100, you can calculate the tax amount: 6% of $100 is $6. The total cost would be $100 + $6 = $106.
3. Investment Returns:
Investors often track their returns as percentages. If an investment of $500 grows to $600, the percentage increase is calculated by finding the increase ($100) and dividing it by the original investment ($500): ($100/$500) × 100% = 20%.
4. Grade Calculations:
Students often need to calculate their overall grade based on weighted percentages of assignments. Understanding percentages helps determine the final score accurately.
5. Statistical Analysis:
Percentages are frequently used in statistics to represent data proportions and trends. Understanding percentage calculations is fundamental to analyzing and interpreting statistical information.
Expanding Your Understanding: Working with Different Percentages
The methods described above can be applied to any percentage problem. For example, let's consider the question: "80 is 40% of what number?" Using the percentage formula:
80 = 0.40 * x
x = 80 / 0.40
x = 200
Therefore, 80 is 40% of 200. This demonstrates the versatility of these methods in handling various percentage calculations.
Beyond Basic Percentages: More Complex Scenarios
While the examples above focus on straightforward percentage calculations, the underlying principles extend to more complex situations. Consider scenarios involving compound interest, exponential growth, and more intricate statistical analysis. Proficiency in basic percentage calculations forms a strong foundation for tackling these advanced problems.
Conclusion: Mastering the Art of Percentage Calculations
The ability to solve problems like "60 is 25% of what number?" is a fundamental skill with wide-ranging applications. By understanding the different methods outlined – using the percentage formula, setting up proportions, employing decimal equivalents, and utilizing an algebraic approach – you'll be well-equipped to handle a variety of percentage-related challenges in your daily life, academic pursuits, and professional endeavors. The key takeaway is to understand the core relationship between parts, percentages, and the whole, and to choose the method most comfortable and efficient for you. Remember to always double-check your work to ensure accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.