60 Is The Least Common Multiple Of 15 And
News Co
Mar 26, 2025 · 5 min read
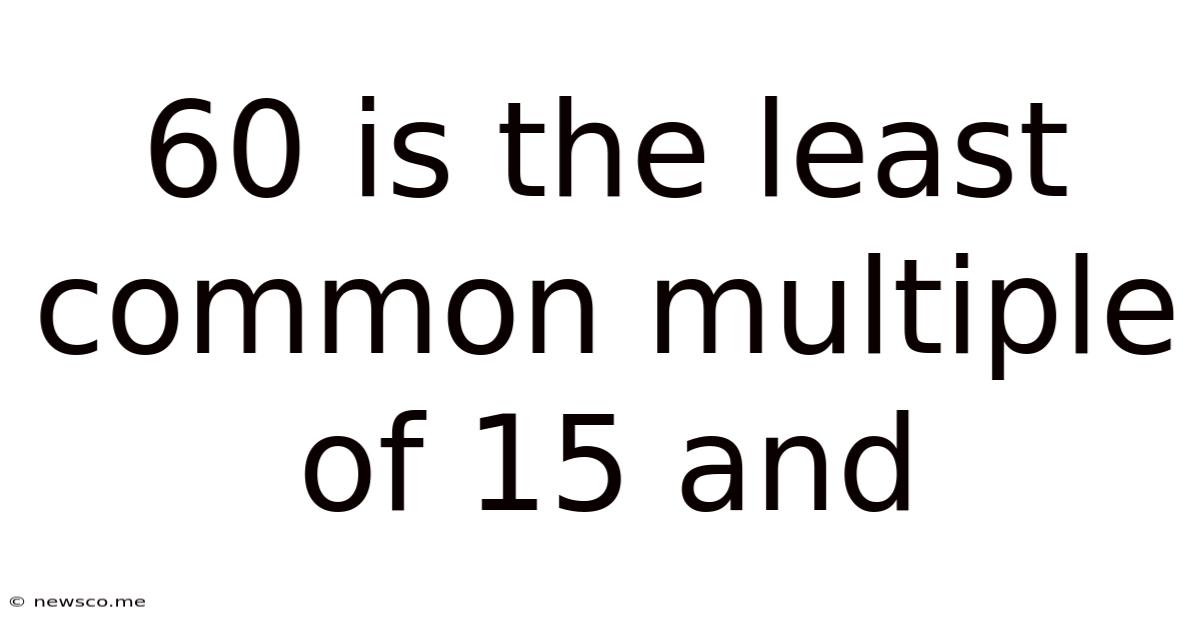
Table of Contents
60 is the Least Common Multiple (LCM) of 15 and...? Unlocking the Secrets of LCM and Finding the Missing Number
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to scheduling events. This article delves into the question: "60 is the least common multiple of 15 and...?" We'll not only find the answer but also explore the underlying principles of LCM, its calculation methods, and real-world applications.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Finding the Missing Number: A Step-by-Step Approach
We know that 60 is the LCM of 15 and another number, let's call it 'x'. To find 'x', we'll utilize several methods.
Method 1: Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
- Prime Factorize 60: 60 = 2² x 3 x 5
- Prime Factorize 15: 15 = 3 x 5
Notice that 15 is already a factor of 60. The prime factorization of 60 includes all the prime factors of 15. The missing factor in the prime factorization of 15 to reach 60 is 2². Therefore, 'x' must contain these missing factors.
- Determine 'x': Since 15 already contains 3 x 5, the only remaining factors are 2². Therefore, x = 2² = 4.
Therefore, 60 is the least common multiple of 15 and 4.
Method 2: Listing Multiples
This is a more straightforward, albeit less efficient method for larger numbers.
- List the multiples of 15: 15, 30, 45, 60, 75, 90, 105...
- List the multiples of 'x' (the unknown number): We need to find a number whose multiples include 60.
By comparing the lists, we find that 60 appears in the multiples of 15, indicating that the LCM is indeed 60. The number 'x' must be a factor of 60 that, when combined with 15, yields an LCM of 60. Through trial and error (or by considering the factors of 60), we find that x = 4.
Method 3: Using the Formula
The formula for finding the LCM of two numbers 'a' and 'b' is:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where GCD stands for the greatest common divisor.
- We know LCM(15, x) = 60.
- Find the GCD(15, x): We know that the GCD of 15 and x must be a factor of 15 (1, 3, 5, 15).
- Substitute and solve: Let's test different GCD values:
- If GCD(15, x) = 1: 60 = (15 * x) / 1 => x = 4
- If GCD(15, x) = 3: 60 = (15 * x) / 3 => x = 12
- If GCD(15, x) = 5: 60 = (15 * x) / 5 => x = 20
- If GCD(15, x) = 15: 60 = (15 * x) / 15 => x = 60
Now we must consider the least common multiple. If x = 12, LCM(15, 12) = 60. If x = 20, LCM(15, 20) = 60. If x = 60, LCM(15, 60) = 60. However, the question asks for the least common multiple. Therefore, only x = 4 fits the criteria of resulting in an LCM of 60 and being the smallest possible value.
Real-World Applications of LCM
The concept of LCM extends far beyond abstract mathematical exercises. It finds practical applications in numerous scenarios:
-
Scheduling: Imagine you have two machines that complete a task in 15 minutes and 'x' minutes, respectively. The LCM determines when both machines will finish a task simultaneously. If one machine takes 15 minutes and the other takes 4 minutes, then they will both finish at the same time after 60 minutes (the LCM of 15 and 4).
-
Fraction Addition and Subtraction: Finding the LCM of denominators is essential when adding or subtracting fractions with different denominators. It allows you to find a common denominator for simplification.
-
Patterning and Sequencing: LCM plays a role in identifying patterns and sequences that repeat at specific intervals.
-
Gear Ratios and Mechanical Systems: In engineering, the LCM is crucial in calculating gear ratios and synchronizing the movements of different components in mechanical systems.
Extending the Concept: LCM of More Than Two Numbers
The principles discussed above can be extended to finding the LCM of more than two numbers. The prime factorization method remains highly effective. Simply find the prime factorization of each number and then take the highest power of each prime factor present in the factorizations.
For example, finding the LCM of 12, 18, and 30:
-
Prime Factorization:
- 12 = 2² x 3
- 18 = 2 x 3²
- 30 = 2 x 3 x 5
-
Identify Highest Powers: The highest power of 2 is 2², the highest power of 3 is 3², and the highest power of 5 is 5.
-
Calculate LCM: LCM(12, 18, 30) = 2² x 3² x 5 = 180
Conclusion: Mastering LCM for Mathematical Proficiency and Real-World Success
Understanding and calculating the least common multiple is a crucial skill in mathematics. This article has not only answered the question, "60 is the least common multiple of 15 and...?" but also provided a comprehensive exploration of LCM, including various calculation methods and its practical applications. Mastering LCM enhances your mathematical proficiency and equips you to tackle real-world problems efficiently across diverse fields. The ability to find LCM efficiently, whether using prime factorization, listing multiples, or the LCM formula, is an invaluable skill that will serve you well in various mathematical and practical situations. Remember to choose the method that best suits your needs and the complexity of the numbers involved.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Is The Least Common Multiple Of 15 And . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.