60 Of 25 Is What Number
News Co
Mar 17, 2025 · 5 min read
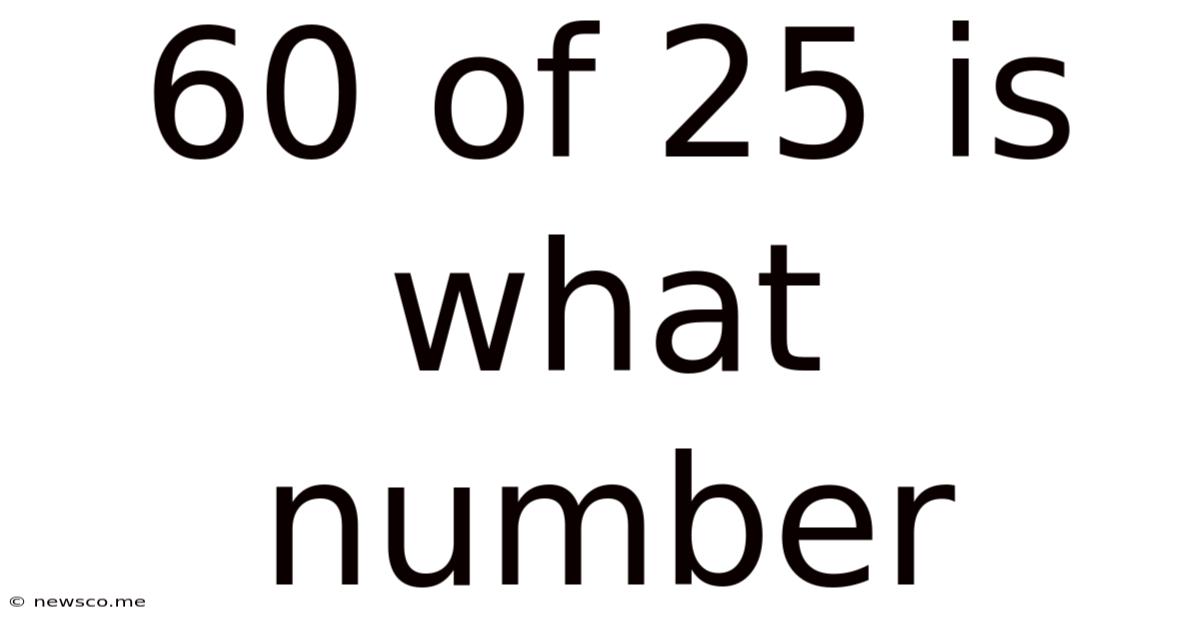
Table of Contents
60% of 25: A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. This article provides a comprehensive exploration of how to calculate 60% of 25, explaining the process step-by-step, exploring different methods, and demonstrating the broader application of percentage calculations. We’ll also delve into the underlying mathematical principles and offer practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 60% represents 60 parts out of 100, or 60/100. This can be simplified to 3/5. This fundamental understanding is crucial for tackling percentage calculations effectively.
Method 1: Converting Percentage to Decimal
The most straightforward approach to calculating 60% of 25 is by converting the percentage into a decimal. To do this, divide the percentage by 100:
60% ÷ 100 = 0.60
Now, multiply this decimal by the number you want to find the percentage of:
0.60 * 25 = 15
Therefore, 60% of 25 is 15.
Method 2: Using Fractions
As mentioned earlier, 60% can be expressed as the fraction 60/100, which simplifies to 3/5. This method involves multiplying the fraction by the number:
(3/5) * 25 = 15
This method highlights the inherent fractional nature of percentages and provides an alternative approach to the calculation. This method is particularly useful when dealing with percentages that are easily converted into simpler fractions.
Method 3: Proportion Method
This method utilizes the concept of proportions to solve for the unknown value. We can set up a proportion:
60/100 = x/25
Where 'x' represents 60% of 25. To solve for 'x', we cross-multiply:
60 * 25 = 100 * x
1500 = 100x
x = 1500/100
x = 15
Again, we arrive at the solution: 60% of 25 is 15. This method emphasizes the proportional relationship between percentages and their corresponding values.
Real-World Applications: Why This Matters
Understanding how to calculate percentages is not just an academic exercise; it has far-reaching applications in various aspects of daily life and professional contexts. Here are some examples:
-
Shopping and Discounts: Calculating discounts on sale items. If a store offers a 60% discount on a $25 item, you can quickly determine the final price using the methods described above.
-
Tax Calculations: Determining the amount of sales tax or income tax payable. Understanding percentages is essential for accurately calculating and budgeting for taxes.
-
Financial Analysis: Analyzing financial statements, calculating investment returns, and understanding interest rates all involve percentage calculations.
-
Statistics and Data Analysis: Percentages are widely used to represent data in charts, graphs, and reports, making it easier to visualize and interpret information.
-
Tip Calculations: Calculating the appropriate tip amount in restaurants and other service-oriented businesses.
-
Grade Calculations: Understanding your performance in school, whether it's calculating your overall grade or determining the weighted average of different assignments.
-
Scientific Applications: In many scientific fields, percentages are used to express concentrations, error margins, and other essential data points.
Expanding Your Percentage Skills: Beyond the Basics
While calculating 60% of 25 is a relatively simple problem, the underlying principles can be applied to more complex scenarios. Consider these extensions:
-
Calculating the Percentage of a Larger Number: The methods described above work equally well with larger numbers. For example, calculating 60% of 250 would follow the same steps, resulting in an answer of 150.
-
Calculating a Different Percentage: If you need to calculate a different percentage of 25 (e.g., 35% of 25), you would simply substitute the new percentage (35/100 or 0.35) into the calculations.
-
Finding the Original Number: You can also use these methods in reverse. If you know that 60% of a number is 15, you can solve for the original number using algebraic techniques.
-
Compound Percentages: This involves applying percentages repeatedly. For example, a 10% increase followed by a 10% decrease does not result in the original value. Understanding compound percentages is crucial in financial planning and investment analysis.
Common Mistakes to Avoid
When working with percentages, be mindful of these common pitfalls:
-
Incorrect Decimal Conversion: Ensure you correctly convert the percentage to a decimal before performing calculations. A simple error here can significantly impact your results.
-
Misinterpreting the Problem: Carefully read the problem statement to understand what percentage you need to calculate and what number it applies to.
-
Order of Operations: Follow the standard order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Rounding Errors: When rounding numbers during calculations, be aware that this can introduce minor inaccuracies in the final result.
-
Confusing Percentage Change with Percentage Points: Percentage points represent the absolute difference between two percentages, while a percentage change refers to the relative change.
Practice Problems
To solidify your understanding, try solving these practice problems:
- Calculate 20% of 75.
- What percentage of 50 is 10?
- If a $100 item is discounted by 15%, what is the final price?
- Calculate 8% of 125.
- A student scores 85% on a test with 40 questions. How many questions did they answer correctly?
Conclusion
Mastering percentage calculations is a valuable skill with widespread applications. By understanding the different methods and avoiding common mistakes, you can confidently tackle percentage problems of varying complexity. The ability to perform these calculations accurately is essential for success in various academic, professional, and personal endeavors. Remember to practice regularly to reinforce your understanding and build confidence in your abilities. Through consistent practice and a clear understanding of the underlying principles, you’ll be well-equipped to navigate the world of percentages with ease.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Of 25 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.