60 Percent Of What Number Is 24
News Co
Apr 13, 2025 · 4 min read
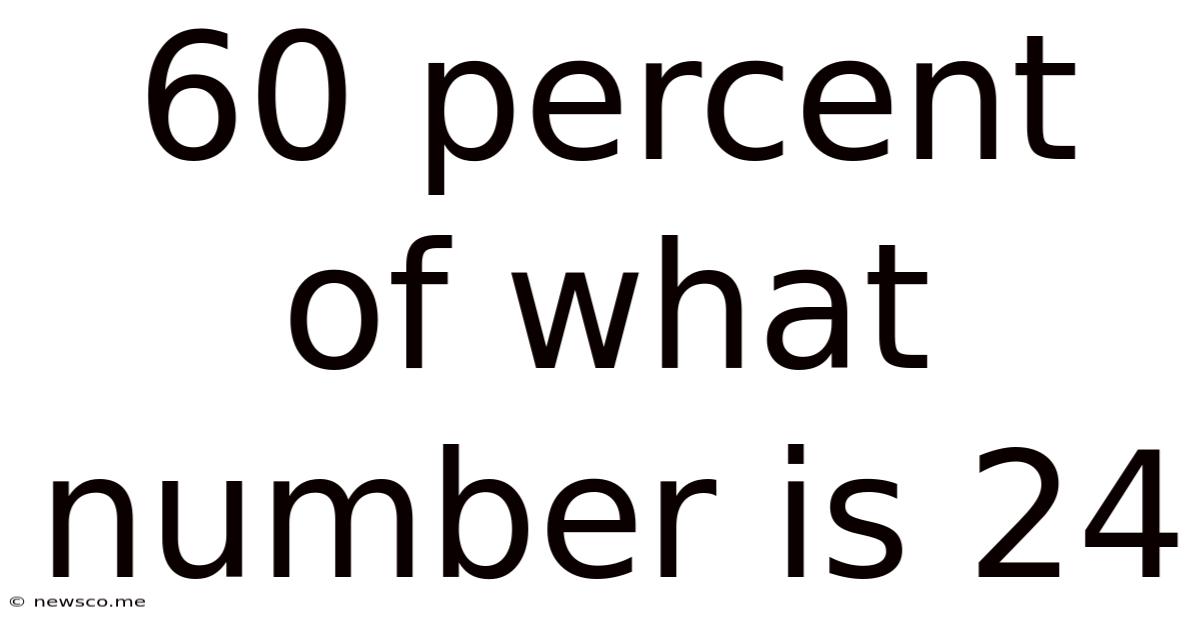
Table of Contents
60 Percent of What Number is 24? Unraveling the Math and its Applications
Finding the answer to "60 percent of what number is 24?" might seem like a simple math problem, but understanding the underlying concepts and applying the solution in various scenarios opens up a world of practical applications. This comprehensive guide will not only provide the solution but also delve into the methods, variations, and real-world examples to solidify your understanding of percentage calculations.
Understanding Percentages
Before diving into the specific problem, let's establish a firm grasp of what percentages represent. A percentage is a fraction or ratio expressed as a number out of 100. It represents a portion of a whole. For instance, 60% means 60 out of 100, or 60/100, which simplifies to 3/5.
Solving "60 Percent of What Number is 24?"
We can tackle this problem using several methods:
Method 1: Algebraic Approach
This method involves setting up an equation and solving for the unknown. Let's represent the unknown number as 'x'. The problem can be expressed as:
0.60x = 24
To solve for x, we divide both sides of the equation by 0.60:
x = 24 / 0.60
x = 40
Therefore, 60 percent of 40 is 24.
Method 2: Using Proportions
This method uses the concept of equivalent ratios. We can set up a proportion:
60/100 = 24/x
To solve for x, we cross-multiply:
60x = 2400
x = 2400 / 60
x = 40
Again, we find that the answer is 40.
Method 3: Working Backwards from the Percentage
Since 60% represents 24, we can find the value of 1% by dividing 24 by 60:
24 / 60 = 0.4
This means 1% of the number is 0.4. To find the whole number (100%), we multiply 0.4 by 100:
0.4 * 100 = 40
This confirms that the number is 40.
Real-World Applications
Understanding percentage calculations like this one has numerous practical applications in everyday life and various professional fields. Here are a few examples:
1. Retail and Sales
Discounts, markups, and sales tax calculations heavily rely on percentages. For example, a store offering a 60% discount on an item could use this calculation to determine the sale price if the original price was unknown but the discounted price was known.
Example: A store sells a jacket for $24 after applying a 60% discount. Using the knowledge that 60% of the original price was $24, the store can determine the original price was $40.
2. Finance and Investments
Percentage changes in investment values, interest rates, and loan calculations are crucial. For example, determining the principal amount of an investment based on the interest earned requires percentage calculations.
Example: If an investment earned $24 in interest, representing 60% of the total interest, the calculation determines the total interest earned was $40.
3. Data Analysis and Statistics
Percentages are fundamental in analyzing data and interpreting statistics. Representing proportions, rates, and changes within datasets commonly involves percentage calculations.
Example: If 24 survey respondents (60% of the sample) answered "yes" to a question, this calculation would help determine the total number of survey respondents (40).
4. Science and Engineering
Percentage calculations are essential in scientific and engineering computations. For instance, determining the concentration of a solution or efficiency of a process may involve percentage calculations.
Example: If 24 milliliters of a chemical solution is 60% of the total solution, calculating the total volume (40 milliliters) is critical in preparing the solution.
Variations and Extensions
The problem "60 percent of what number is 24" can be modified to explore similar scenarios:
-
Different Percentage: Instead of 60%, we could use other percentages, such as 25%, 75%, or even a decimal representation like 0.6. The same methods apply.
-
Different Result: Instead of 24, we could change the result to another number and solve for a new unknown value.
-
More Complex Scenarios: We could incorporate additional variables or steps into the problem, making it more challenging but still solvable using the same fundamental principles. For example, if we added a tax percentage on top of the discount, the problem would require multiple steps.
Conclusion
The seemingly simple question, "60 percent of what number is 24?", unlocks a wealth of understanding regarding percentage calculations and their far-reaching applications. By mastering the algebraic, proportional, and reverse percentage methods, individuals can confidently solve such problems and apply them to various real-world situations. From analyzing sales data to managing finances, the ability to calculate percentages accurately enhances decision-making and problem-solving skills across numerous fields. The core principles remain consistent, making the application of percentages versatile and valuable in navigating various aspects of life and work. Understanding these calculations empowers individuals to interpret data, analyze trends, and confidently solve real-world challenges involving proportions and ratios.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Percent Of What Number Is 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.