.625 As A Fraction Step By Step
News Co
Apr 03, 2025 · 5 min read
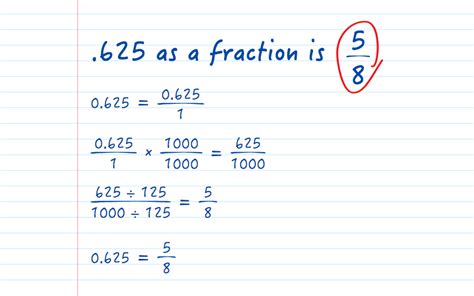
Table of Contents
.625 as a Fraction: A Step-by-Step Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the decimal 0.625 into a fraction, explaining each step in detail. We'll also explore various methods and delve into the underlying principles, making this concept clear and accessible to everyone, from beginners to those seeking a refresher.
Understanding Decimals and Fractions
Before we begin the conversion, let's refresh our understanding of decimals and fractions.
-
Decimals: Decimals represent parts of a whole using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.625 represents 6 tenths, 2 hundredths, and 5 thousandths.
-
Fractions: Fractions represent parts of a whole as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts.
Method 1: Using the Place Value Method
This method leverages the place value of the decimal digits to directly write the fraction.
Step 1: Identify the Place Value of the Last Digit
In the decimal 0.625, the last digit, 5, is in the thousandths place. This means the denominator of our fraction will be 1000 (10³).
Step 2: Write the Decimal as a Numerator
Simply remove the decimal point and use the digits as the numerator of the fraction. In this case, the numerator becomes 625.
Step 3: Form the Fraction
Combine the numerator and denominator to form the fraction: 625/1000.
Step 4: Simplify the Fraction
This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 625 and 1000 is 125. Divide both the numerator and denominator by 125:
625 ÷ 125 = 5 1000 ÷ 125 = 8
Therefore, the simplified fraction is 5/8.
Method 2: Using the Equivalent Fraction Method
This method involves expressing the decimal as an equivalent fraction with a power of 10 as the denominator.
Step 1: Write the Decimal as a Fraction with a Power of 10 as the Denominator
As we determined earlier, the decimal 0.625 has a thousandths place as its last digit. Therefore, we can write it as 625/1000.
Step 2: Simplify the Fraction
This step is identical to Step 4 in Method 1. Find the GCD of 625 and 1000 (which is 125) and divide both the numerator and the denominator by it.
625 ÷ 125 = 5 1000 ÷ 125 = 8
This gives us the simplified fraction of 5/8.
Method 3: Repeated Division Method (for more complex decimals)
While the previous methods work perfectly for this specific decimal, the repeated division method is useful for more complex decimals that might not have an easily identifiable power-of-ten denominator.
Step 1: Write the decimal as a fraction over 1.
0.625/1
Step 2: Multiply the numerator and denominator by a power of 10 to eliminate the decimal point.
Multiply both by 1000 to move the decimal point three places to the right:
(0.625 x 1000) / (1 x 1000) = 625/1000
Step 3: Find the greatest common divisor (GCD) of the numerator and denominator and simplify.
Again, the GCD of 625 and 1000 is 125. Dividing both by 125 gives us the simplified fraction: 5/8.
Verifying the Result
To ensure our conversion is accurate, we can convert the fraction 5/8 back to a decimal. Divide the numerator (5) by the denominator (8):
5 ÷ 8 = 0.625
This confirms that our conversion from 0.625 to 5/8 is correct.
Understanding the Importance of Simplification
Simplifying fractions is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and work with. 5/8 is much clearer than 625/1000.
- Comparison: Simplified fractions allow for easier comparison of different fractions.
- Efficiency: Simplified fractions make calculations more efficient.
Advanced Applications and Extensions
The principles used to convert 0.625 to a fraction can be extended to convert other decimals, including those with repeating decimals (e.g., 0.333...). While repeating decimals require a slightly different approach, the underlying concept of finding equivalent fractions remains the same. Learning to convert between decimals and fractions is invaluable for various mathematical applications, including:
- Algebra: Solving equations and simplifying expressions often requires working with both decimals and fractions.
- Geometry: Calculating areas, volumes, and other geometric properties frequently involve fractions.
- Calculus: Understanding fractions is essential for many calculus concepts, such as limits and derivatives.
- Data Analysis: Representing and interpreting data often requires working with both decimals and fractions.
Practical Examples in Everyday Life
Converting decimals to fractions isn't just an academic exercise; it has practical applications in everyday life:
- Cooking: Recipes often use fractions (e.g., 1/2 cup of sugar). Understanding the equivalent decimal can be helpful when using measuring tools.
- Construction: Measurements in construction often involve fractions of inches or feet.
- Finance: Calculating percentages and proportions in finance frequently requires working with fractions and decimals.
Conclusion
Converting the decimal 0.625 to the fraction 5/8, as shown through various methods, highlights the fundamental relationship between decimals and fractions. Mastering this conversion skill is essential for success in various mathematical fields and in everyday life situations. Remember that simplification is key to clarity and efficiency when working with fractions. By understanding the underlying principles and practicing these different methods, you can confidently tackle decimal-to-fraction conversions of varying complexity. The more you practice, the quicker and more intuitive this process will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about .625 As A Fraction Step By Step . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.