63 Is 45 Of What Number
News Co
May 07, 2025 · 4 min read
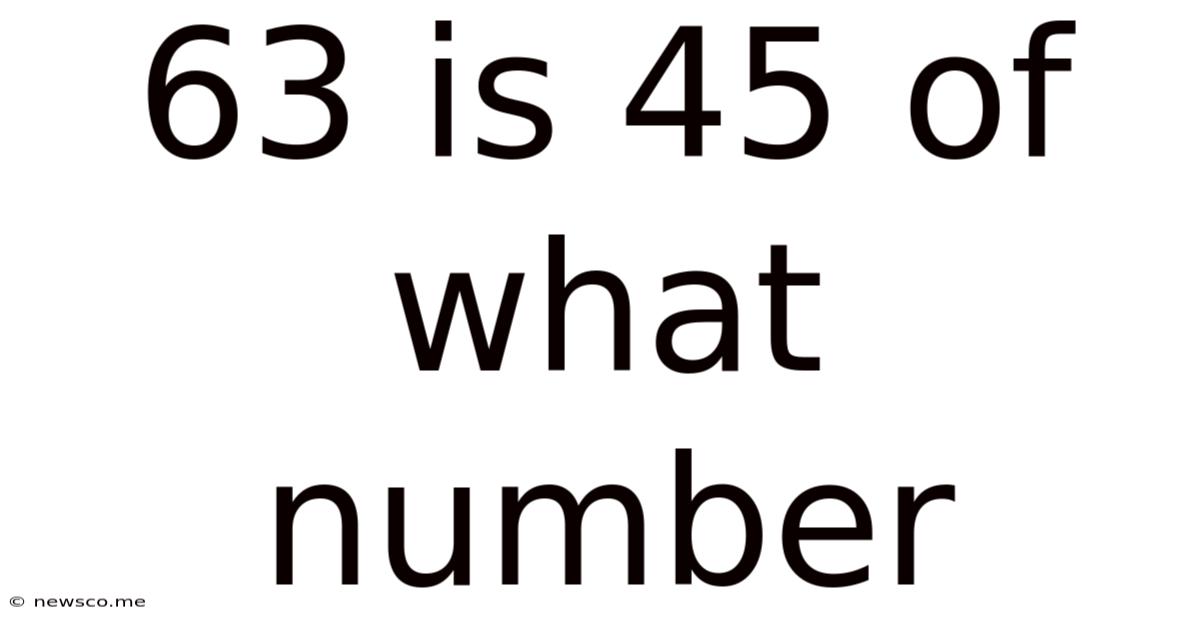
Table of Contents
63 is 45% of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex scientific calculations and business analysis. This article delves into the question, "63 is 45% of what number?", providing a step-by-step solution, exploring different approaches, and examining the broader context of percentage calculations. We'll also explore practical applications and offer helpful tips to master these types of problems.
Understanding Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of one hundred." Therefore, 45% can be written as 45/100 or 0.45.
Method 1: Algebraic Approach
This is the most common and generally preferred method for solving percentage problems like this. We can translate the problem into an algebraic equation:
- Let 'x' represent the unknown number.
- "63 is 45% of what number?" translates to: 63 = 0.45x
Now, we solve for 'x':
- Divide both sides of the equation by 0.45: x = 63 / 0.45
- Perform the division: x = 140
Therefore, 63 is 45% of 140.
This algebraic method offers a structured and easily understandable approach, especially when dealing with more complex percentage problems. It emphasizes the fundamental relationship between percentages, fractions, and decimals, strengthening your overall understanding of mathematical concepts.
Method 2: Using Proportions
The proportion method offers an alternative approach, equally effective in solving percentage problems. We can set up a proportion as follows:
- Part/Whole = Percentage/100
In our problem:
- Part = 63
- Percentage = 45
- Whole = x (the unknown number)
Substituting these values into the proportion equation, we get:
63/x = 45/100
Now, we solve for 'x' using cross-multiplication:
- Cross-multiply: 63 * 100 = 45 * x
- Simplify: 6300 = 45x
- Divide both sides by 45: x = 6300 / 45
- Perform the division: x = 140
Again, we find that 63 is 45% of 140. This method provides a visual representation of the relationship between the parts and the whole, making it particularly useful for visualizing percentage problems.
Method 3: Working with Fractions
We can also solve this problem by working directly with fractions. Remember that 45% is equivalent to 45/100. The problem can be restated as:
63 = (45/100) * x
Solving for x:
- Multiply both sides by 100: 6300 = 45x
- Divide both sides by 45: x = 6300 / 45
- Perform the division: x = 140
This approach emphasizes the fundamental connection between percentages and fractions, helping you build a stronger understanding of mathematical equivalencies. This method can be particularly helpful when dealing with percentages that are easily expressed as simple fractions.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
1. Finance and Budgeting:
- Calculating discounts: Determining the actual price after a discount is applied. For example, a 20% discount on a $100 item.
- Calculating interest: Determining the amount of interest earned on savings or owed on loans.
- Analyzing financial statements: Understanding profit margins, growth rates, and other key financial metrics expressed as percentages.
2. Sales and Marketing:
- Tracking conversion rates: Measuring the effectiveness of marketing campaigns by calculating the percentage of visitors who convert into customers.
- Analyzing market share: Determining the percentage of the market a company controls.
- Setting sales targets: Establishing goals expressed as a percentage increase in sales revenue.
3. Science and Research:
- Statistical analysis: Calculating percentages in data analysis, hypothesis testing, and other statistical methods.
- Expressing experimental results: Presenting results as percentages to show the proportion of successful outcomes or changes observed.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants or for service providers.
- Understanding sales tax: Calculating the total cost of an item including sales tax.
- Comparing prices: Determining the best value by comparing prices and discounts expressed as percentages.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with different approaches and problem types.
- Understand the underlying concepts: Ensure you have a solid understanding of fractions, decimals, and their relationship to percentages.
- Use different methods: Experiment with different methods (algebraic, proportion, fractions) to find the approach that suits your learning style best.
- Check your work: Always double-check your calculations to ensure accuracy.
- Use online resources: Many websites and apps offer practice problems and tutorials on percentage calculations.
Conclusion
Solving problems like "63 is 45% of what number?" is more than just a mathematical exercise; it's a fundamental skill with far-reaching applications. By mastering these calculations, you equip yourself with a valuable tool for navigating various aspects of daily life, professional endeavors, and academic pursuits. Remember to practice regularly, utilize different approaches, and maintain a strong understanding of the underlying concepts to build confidence and proficiency in solving percentage problems. The more you work with these concepts, the more intuitive they will become, making complex percentage calculations straightforward and efficient. This empowers you to analyze data, make informed decisions, and excel in numerous contexts where percentage understanding is paramount.
Latest Posts
Latest Posts
-
Equivalencia 180 Grados Farenheit A Centigrados
May 07, 2025
-
1 5 On The Number Line
May 07, 2025
-
Each Set Of Place Value Blocks Below Represents A Decimal
May 07, 2025
-
Definition Of Congruent Circles In Geometry
May 07, 2025
-
If A Number Is Real Then It Is Also Rational
May 07, 2025
Related Post
Thank you for visiting our website which covers about 63 Is 45 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.