66 And 2/3 Percent As A Fraction
News Co
Apr 03, 2025 · 5 min read
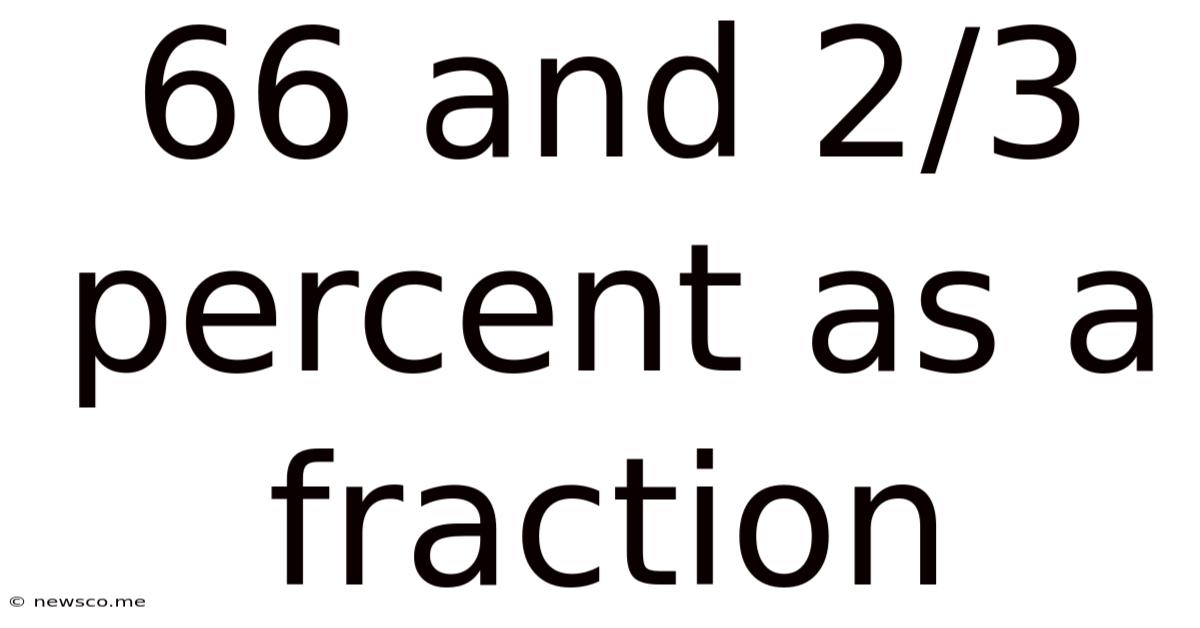
Table of Contents
66 and 2/3 Percent as a Fraction: A Comprehensive Guide
Understanding percentages and their fractional equivalents is a fundamental skill in mathematics, with applications spanning various fields from finance and cooking to construction and data analysis. This comprehensive guide delves into the intricacies of converting 66 and 2/3 percent into a fraction, exploring different methods and providing a solid foundation for tackling similar conversions. We'll move beyond the simple conversion, examining the practical applications and demonstrating why understanding this concept is crucial for numerical proficiency.
Understanding Percentages and Fractions
Before diving into the conversion, let's solidify our understanding of percentages and fractions. A percentage is a way of expressing a number as a fraction of 100. The percent symbol (%) signifies "per hundred." For example, 50% means 50 out of 100, or 50/100.
A fraction, on the other hand, represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one part out of two equal parts.
The relationship between percentages and fractions is direct: a percentage can always be expressed as a fraction with a denominator of 100, and a fraction can be converted into a percentage.
Converting 66 and 2/3 Percent to a Fraction: Step-by-Step
The conversion of 66 and 2/3% to a fraction involves several steps:
Step 1: Convert the mixed number percentage to an improper fraction.
First, we need to transform the mixed number percentage, 66 and 2/3%, into an improper fraction. To do this, we multiply the whole number (66) by the denominator (3) and add the numerator (2). This result becomes the new numerator, while the denominator remains the same.
66 x 3 + 2 = 198 + 2 = 200
Therefore, 66 and 2/3% becomes 200/3%.
Step 2: Express the percentage as a fraction with a denominator of 100.
Remember that the percent symbol (%) means "per hundred." Thus, 200/3% can be written as 200/3 out of 100, which is expressed as a fraction:
200/3 / 100
Step 3: Simplify the complex fraction.
To simplify this complex fraction, we can multiply the numerator by the reciprocal of the denominator (flipping the denominator fraction). The reciprocal of 100 is 1/100.
(200/3) * (1/100) = 200/300
Step 4: Simplify the fraction to its lowest terms.
We can now simplify the fraction 200/300 by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 200 and 300 is 100. Dividing both the numerator and the denominator by 100 gives us:
200/300 = 2/3
Therefore, 66 and 2/3 percent is equivalent to the fraction 2/3.
Alternative Method: Direct Conversion
Alternatively, we can convert the mixed number percentage to a decimal and then convert the decimal to a fraction.
Step 1: Convert the mixed number to a decimal.
First convert 2/3 to a decimal by dividing 2 by 3, resulting in approximately 0.6667 (we'll use more decimal places for greater accuracy in later steps).
Step 2: Add the whole number.
Add this decimal to the whole number: 66 + 0.6667 = 66.6667
Step 3: Convert the decimal to a fraction.
To convert 66.6667 to a fraction, we can write it as 66.6667/1. Then, we multiply both the numerator and denominator by 10000 to remove the decimal point:
666667/10000
Step 4: Simplify the fraction.
This fraction can be simplified further. However, finding the greatest common divisor for large numbers can be challenging. In such cases, using a calculator or online tools to find the GCD can help. In this case, the simplification is not immediately obvious without a calculator and leads to an approximation anyway. The direct method shown earlier is often more efficient.
While this method works, it's less efficient and is more prone to rounding errors, especially when dealing with repeating decimals like the one resulting from 2/3.
Practical Applications of Converting Percentages to Fractions
The ability to convert percentages to fractions is essential in numerous real-world situations:
-
Cooking and Baking: Many recipes use fractions to specify ingredient amounts. Understanding how to convert percentages, perhaps from a nutritional label, to fractions is crucial for accurate measurements.
-
Construction and Engineering: Calculations involving dimensions, ratios, and material quantities often require working with fractions. Converting percentages from blueprints or specifications to fractions ensures precise calculations.
-
Finance and Investment: Understanding percentage changes in stock prices, interest rates, or profit margins often requires conversion to fractions to perform accurate calculations and comparisons.
-
Data Analysis and Statistics: Data is often represented using percentages. Converting these percentages to fractions allows for simpler calculations and manipulations when performing statistical analyses.
Beyond the Conversion: Working with Fractions and Percentages
Mastering the conversion of percentages to fractions is just the first step. Developing proficiency in working with fractions themselves is equally vital. This includes:
-
Adding and Subtracting Fractions: Understanding common denominators is essential for accurately combining or comparing fractional values.
-
Multiplying and Dividing Fractions: These operations are fundamental in various mathematical contexts and require understanding the rules of fraction manipulation.
-
Simplifying Fractions: Reducing fractions to their lowest terms makes calculations easier and results clearer.
-
Converting between Improper and Mixed Fractions: Fluency in moving between these two representations is crucial for efficient problem-solving.
Understanding and applying these skills builds a robust foundation in mathematical literacy, essential for success in numerous academic and professional pursuits.
Conclusion: The Importance of Numerical Fluency
The conversion of 66 and 2/3 percent to the fraction 2/3 is more than a simple mathematical exercise. It's a demonstration of the interconnectedness of different numerical representations and highlights the importance of numerical fluency. This skill extends far beyond the classroom, impacting various aspects of daily life and professional endeavors. By mastering the concepts discussed in this guide, you enhance your mathematical proficiency and unlock a deeper understanding of the world around you. The ability to effortlessly translate between percentages and fractions empowers you to tackle complex problems with confidence and accuracy. Remember, practice is key; the more you work with these conversions, the more intuitive and effortless they will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 66 And 2/3 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.