7 3 Divided By 3 As A Fraction
News Co
May 08, 2025 · 4 min read
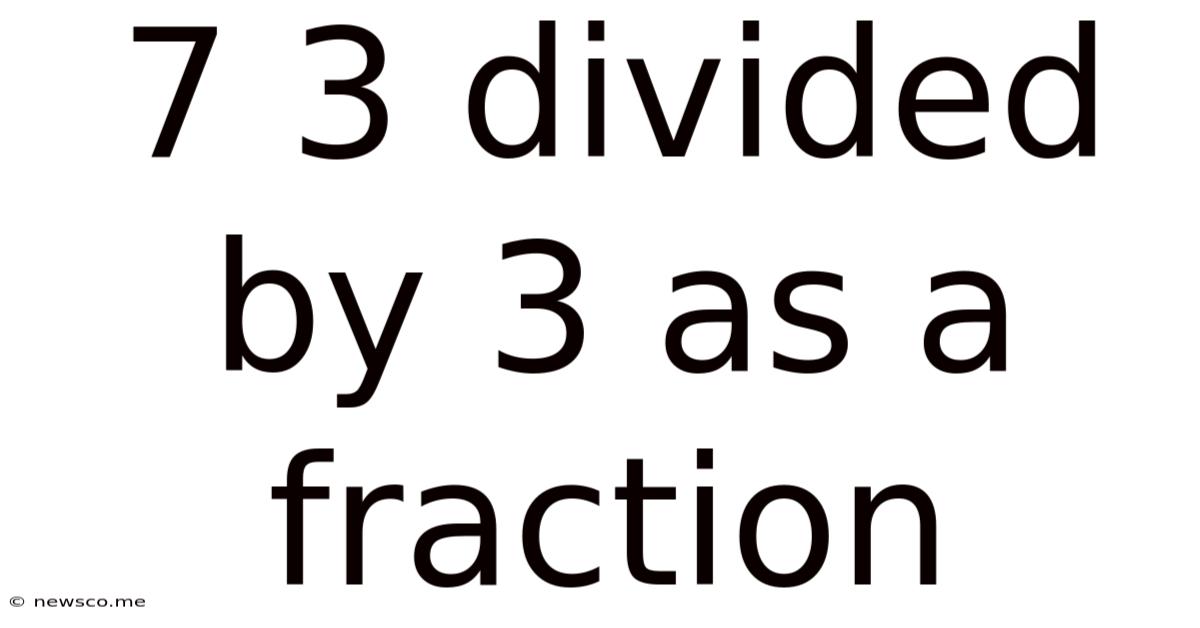
Table of Contents
7 3/3 as a Fraction: A Comprehensive Guide
Understanding fractions is fundamental to mathematics, forming the building blocks for more complex concepts. This article delves into the seemingly simple problem of expressing 7 3/3 as a fraction, exploring the underlying principles and demonstrating various methods for solving similar problems. We'll go beyond a simple answer, providing a thorough understanding of mixed numbers, improper fractions, and the conversion process.
Understanding Mixed Numbers and Improper Fractions
Before tackling 7 3/3, let's clarify some key terms:
-
Mixed Number: A mixed number combines a whole number and a fraction, such as 7 3/3. It represents a quantity greater than one.
-
Improper Fraction: An improper fraction has a numerator (top number) that is greater than or equal to its denominator (bottom number). For instance, 22/7 is an improper fraction.
-
Proper Fraction: A proper fraction has a numerator smaller than its denominator, like 3/7.
Solving 7 3/3: Step-by-Step
The expression 7 3/3 presents a unique opportunity to solidify our understanding of mixed numbers and their conversion to improper fractions. While it might seem straightforward, the process reveals crucial mathematical principles.
Step 1: Focus on the Fractional Part
The key lies in the fraction 3/3. Any number divided by itself equals 1. Therefore, 3/3 simplifies to 1.
Step 2: Substitute and Simplify
Replacing 3/3 with 1 in our original mixed number, we get:
7 3/3 = 7 + 1
Step 3: Final Result
Adding 7 and 1, we arrive at our final answer:
7 + 1 = 8
Therefore, 7 3/3 is equal to 8. While this specific example yields a whole number, the underlying process is essential for handling more complex mixed numbers.
Generalizing the Conversion Process: Mixed Numbers to Improper Fractions
While 7 3/3 provided a simplified example, let's examine the general method for converting any mixed number into an improper fraction. This will equip you with the skills to tackle a wide range of similar problems.
Step 1: Multiply the Whole Number by the Denominator
Take the whole number part of your mixed number and multiply it by the denominator of the fraction. For example, if we have the mixed number 5 2/7, we multiply 5 (the whole number) by 7 (the denominator). This gives us 35.
Step 2: Add the Numerator
Add the result from Step 1 to the numerator of the fraction. In our 5 2/7 example, we add 35 (from Step 1) to 2 (the numerator), resulting in 37.
Step 3: Maintain the Denominator
The denominator of the improper fraction remains the same as the denominator of the original fraction. In our example, the denominator is still 7.
Step 4: Form the Improper Fraction
Combine the results from Steps 2 and 3 to form the improper fraction. For 5 2/7, the improper fraction becomes 37/7.
Example: Converting 4 5/6 to an Improper Fraction
Let's apply the steps above to another mixed number: 4 5/6.
- Multiply whole number by denominator: 4 * 6 = 24
- Add the numerator: 24 + 5 = 29
- Maintain the denominator: The denominator remains 6.
- Form the improper fraction: 29/6
Therefore, 4 5/6 is equivalent to the improper fraction 29/6.
The Importance of Understanding Fraction Conversion
The ability to convert between mixed numbers and improper fractions is crucial for various mathematical operations, including:
-
Addition and Subtraction of Fractions: Adding or subtracting mixed numbers often requires converting them to improper fractions first to simplify the calculation.
-
Multiplication and Division of Fractions: While possible with mixed numbers, converting to improper fractions usually makes these operations simpler and less prone to errors.
-
Solving Algebraic Equations: Many algebraic equations involve fractions, and converting between mixed numbers and improper fractions is a necessary step in the solution process.
-
Real-world Applications: Understanding fractions is essential in various real-world scenarios, from cooking and baking (measuring ingredients) to construction (measuring materials) and finance (calculating proportions).
Advanced Concepts and Further Exploration
While we've covered the basics of converting 7 3/3 and other mixed numbers to fractions, there are more advanced concepts to explore:
-
Simplifying Fractions: After converting a mixed number to an improper fraction, it's often necessary to simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator.
-
Working with Negative Mixed Numbers: The same principles apply when dealing with mixed numbers that have a negative whole number component.
-
Comparing Fractions: Understanding improper fractions allows for easier comparison of fractions with different denominators.
-
Decimal Conversions: Improper fractions can easily be converted to decimals through division.
Conclusion: Mastering Fractions for Mathematical Proficiency
Mastering the conversion between mixed numbers and improper fractions is a cornerstone of mathematical understanding. While the example of 7 3/3 provided a simplified entry point, the principles learned extend far beyond this specific case. By understanding these processes and applying the methods outlined in this article, you'll enhance your mathematical skills, enabling you to tackle more complex problems and apply fractions confidently in various contexts. Remember, practice is key to mastering these fundamental concepts. Work through various examples, challenge yourself with more complex mixed numbers, and soon you'll find fractions become second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about 7 3 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.