7/8 Divided By 2/3 As A Fraction
News Co
Apr 27, 2025 · 4 min read
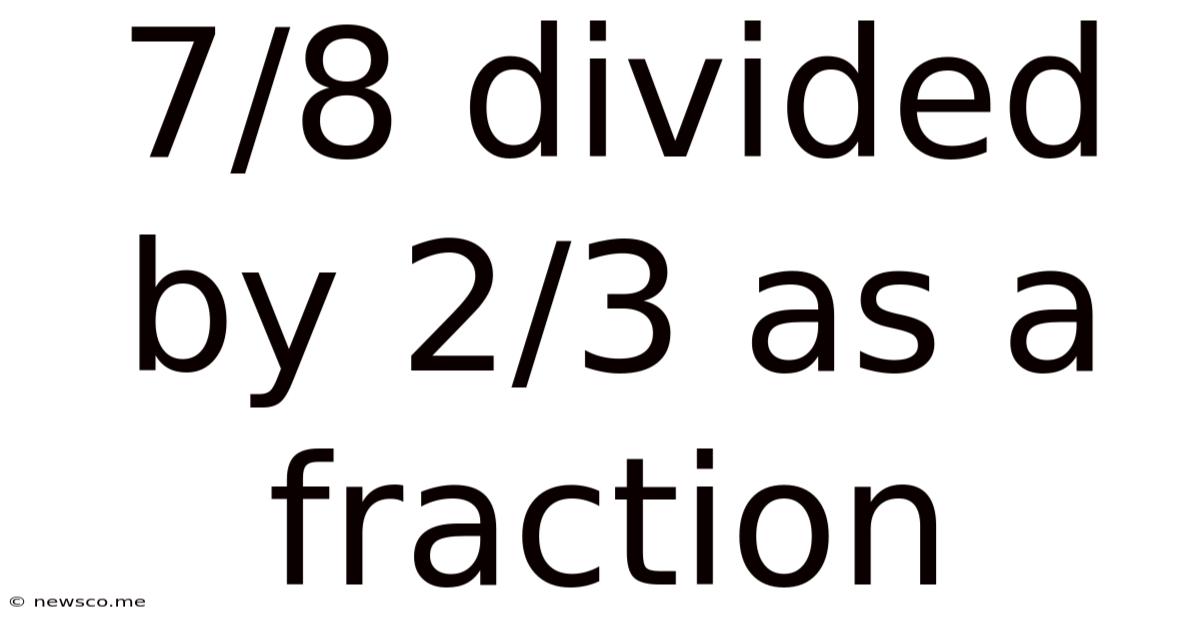
Table of Contents
7/8 Divided by 2/3 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 7/8 by 2/3, explaining the steps involved and providing you with the tools to tackle similar fraction division problems. We'll explore the concept of reciprocals, demonstrate the calculation, and offer practical applications to solidify your understanding. We'll also look at how to check your work and discuss common mistakes to avoid.
Understanding Fraction Division
Before diving into the specific problem of 7/8 divided by 2/3, let's review the fundamental principles of fraction division. The core concept revolves around the idea of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
The key rule for dividing fractions is: To divide a fraction by another fraction, multiply the first fraction by the reciprocal of the second fraction.
This seemingly simple rule is the cornerstone of solving all fraction division problems. Let's break it down further.
Step-by-Step Breakdown of Fraction Division
-
Identify the Fractions: Clearly identify the dividend (the fraction being divided) and the divisor (the fraction you're dividing by). In our case:
- Dividend: 7/8
- Divisor: 2/3
-
Find the Reciprocal: Determine the reciprocal of the divisor (the second fraction). The reciprocal of 2/3 is 3/2.
-
Multiply the Fractions: Now, instead of dividing, we multiply the dividend by the reciprocal of the divisor:
7/8 x 3/2
-
Multiply Numerators and Denominators: Multiply the numerators (top numbers) together and the denominators (bottom numbers) together separately:
(7 x 3) / (8 x 2) = 21/16
-
Simplify (If Possible): Check if the resulting fraction can be simplified. In this case, 21/16 is an improper fraction (the numerator is larger than the denominator). We can leave it as an improper fraction or convert it to a mixed number.
To convert 21/16 to a mixed number, we perform the division: 21 ÷ 16 = 1 with a remainder of 5. Therefore, 21/16 can be written as 1 5/16.
Therefore, 7/8 divided by 2/3 equals 21/16 or 1 5/16.
Visualizing Fraction Division
While the mathematical process is crucial, visualizing the division can enhance understanding. Imagine you have 7/8 of a pizza. Dividing this by 2/3 means finding out how many 2/3 slices you can get from the 7/8 pizza. The calculation shows you can get 1 and 5/16 slices of 2/3 size from your 7/8 pizza.
Practical Applications of Fraction Division
Fraction division appears in numerous real-world scenarios:
- Baking: Adjusting recipes based on the amount of ingredients available.
- Sewing: Calculating fabric requirements for a project.
- Construction: Measuring and cutting materials to precise specifications.
- Gardening: Dividing plants or seeds.
- Cooking: Scaling recipes up or down.
Understanding fraction division is essential for accurate calculations in these and many other contexts.
Checking Your Work
It's always a good practice to verify your answer. One method is to use a calculator with fraction capabilities. Another approach is to estimate the answer. Since 7/8 is slightly less than 1 and 2/3 is slightly more than 1/2, we expect the result to be slightly less than 2 (because 1 divided by 1/2 is 2). Our answer of 1 5/16 fits this estimation.
Common Mistakes to Avoid
- Forgetting to find the reciprocal: This is the most common mistake. Remember, you must multiply by the reciprocal of the divisor, not the divisor itself.
- Incorrect multiplication: Double-check your multiplication of numerators and denominators.
- Failing to simplify: Always simplify your answer to its lowest terms.
Advanced Concepts Related to Fraction Division
While we focused on the basic division of two simple fractions, the principles extend to more complex scenarios:
- Dividing mixed numbers: Convert mixed numbers into improper fractions before applying the division rule.
- Dividing fractions with variables: The same principles apply; simply treat variables like numbers.
- Dividing complex fractions: Simplify the complex fractions to simpler fractions before applying the division rule.
Conclusion
Dividing fractions, particularly 7/8 divided by 2/3, becomes manageable with a structured approach. By understanding the concept of reciprocals and following the step-by-step process, you can confidently solve fraction division problems. Remember to check your work and be mindful of common mistakes. With practice, you'll master this fundamental mathematical skill and apply it to various real-world situations. The result of 7/8 divided by 2/3 is definitively 21/16 or 1 5/16. Mastering this concept will significantly enhance your mathematical abilities and problem-solving skills.
Keywords:
divide fractions, fraction division, 7/8 divided by 2/3, reciprocal, improper fraction, mixed number, fraction calculation, math problem, fraction simplification, real-world applications of fractions, problem-solving, mathematical skills
Semantic Keywords:
fraction arithmetic, basic fractions, advanced fractions, fraction operations, solving math problems, practical mathematics, numerical skills, mathematical concepts, fractional calculations, working with fractions.
Latest Posts
Related Post
Thank you for visiting our website which covers about 7/8 Divided By 2/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.